Jacobian Sparse Autoencoders: Sparsify Computations, Not Just Activations

Sparse autoencoders (SAEs) have been successfully used to discover sparse and human-interpretable representations of the latent activations of LLMs. However, we would ultimately like to understand the computations performed by LLMs and not just their representations. The extent to which SAEs can help us understand computations is unclear because they are not designed to "sparsify" computations in any sense, only latent activations. To solve this, we propose Jacobian SAEs (JSAEs), which yield not only sparsity in the input and output activations of a given model component but also sparsity in the computation (formally, the Jacobian) connecting them. With a na\"ive implementation, the Jacobians in LLMs would be computationally intractable due to their size. One key technical contribution is thus finding an efficient way of computing Jacobians in this setup. We find that JSAEs extract a relatively large degree of computational sparsity while preserving downstream LLM performance approximately as well as traditional SAEs. We also show that Jacobians are a reasonable proxy for computational sparsity because MLPs are approximately linear when rewritten in the JSAE basis. Lastly, we show that JSAEs achieve a greater degree of computational sparsity on pre-trained LLMs than on the equivalent randomized LLM. This shows that the sparsity of the computational graph appears to be a property that LLMs learn through training, and suggests that JSAEs might be more suitable for understanding learned transformer computations than standard SAEs.

Sparse Autoencoders Can Interpret Randomly Initialized Transformers

Sparse autoencoders (SAEs) are an increasingly popular technique for interpreting the internal representations of transformers. In this paper, we apply SAEs to 'interpret' random transformers, i.e., transformers where the parameters are sampled IID from a Gaussian rather than trained on text data. We find that random and trained transformers produce similarly interpretable SAE latents, and we confirm this finding quantitatively using an open-source auto-interpretability pipeline. Further, we find that SAE quality metrics are broadly similar for random and trained transformers. We find that these results hold across model sizes and layers. We discuss a number of number interesting questions that this work raises for the use of SAEs and auto-interpretability in the context of mechanistic interpretability.

Inducing Human-like Biases in Moral Reasoning Language Models

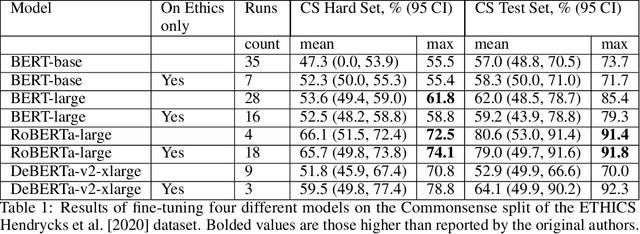
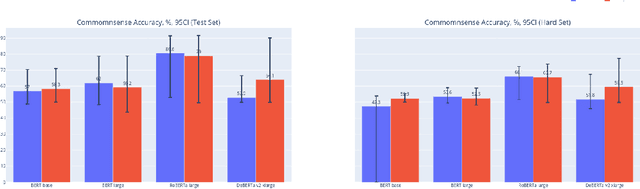
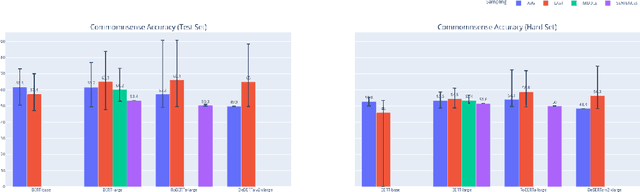
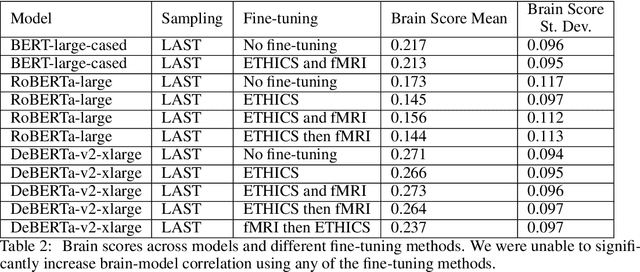
In this work, we study the alignment (BrainScore) of large language models (LLMs) fine-tuned for moral reasoning on behavioral data and/or brain data of humans performing the same task. We also explore if fine-tuning several LLMs on the fMRI data of humans performing moral reasoning can improve the BrainScore. We fine-tune several LLMs (BERT, RoBERTa, DeBERTa) on moral reasoning behavioral data from the ETHICS benchmark [Hendrycks et al., 2020], on the moral reasoning fMRI data from Koster-Hale et al. [2013], or on both. We study both the accuracy on the ETHICS benchmark and the BrainScores between model activations and fMRI data. While larger models generally performed better on both metrics, BrainScores did not significantly improve after fine-tuning.

Residual Stream Analysis with Multi-Layer SAEs

Sparse autoencoders (SAEs) are a promising approach to interpreting the internal representations of transformer language models. However, standard SAEs are trained separately on each transformer layer, making it difficult to use them to study how information flows across layers. To solve this problem, we introduce the multi-layer SAE (MLSAE): a single SAE trained on the residual stream activation vectors from every transformer layer simultaneously. The residual stream is usually understood as preserving information across layers, so we expected to, and did, find individual SAE features that are active at multiple layers. Interestingly, while a single SAE feature is active at different layers for different prompts, for a single prompt, we find that a single feature is far more likely to be active at a single layer. For larger underlying models, we find that the cosine similarities between adjacent layers in the residual stream are higher, so we expect more features to be active at multiple layers. These results show that MLSAEs are a promising method to study information flow in transformers. We release our code to train and analyze MLSAEs at https://github.com/tim-lawson/mlsae.

STARC: A General Framework For Quantifying Differences Between Reward Functions

In order to solve a task using reinforcement learning, it is necessary to first formalise the goal of that task as a reward function. However, for many real-world tasks, it is very difficult to manually specify a reward function that never incentivises undesirable behaviour. As a result, it is increasingly popular to use reward learning algorithms, which attempt to learn a reward function from data. However, the theoretical foundations of reward learning are not yet well-developed. In particular, it is typically not known when a given reward learning algorithm with high probability will learn a reward function that is safe to optimise. This means that reward learning algorithms generally must be evaluated empirically, which is expensive, and that their failure modes are difficult to predict in advance. One of the roadblocks to deriving better theoretical guarantees is the lack of good methods for quantifying the difference between reward functions. In this paper we provide a solution to this problem, in the form of a class of pseudometrics on the space of all reward functions that we call STARC (STAndardised Reward Comparison) metrics. We show that STARC metrics induce both an upper and a lower bound on worst-case regret, which implies that our metrics are tight, and that any metric with the same properties must be bilipschitz equivalent to ours. Moreover, we also identify a number of issues with reward metrics proposed by earlier works. Finally, we evaluate our metrics empirically, to demonstrate their practical efficacy. STARC metrics can be used to make both theoretical and empirical analysis of reward learning algorithms both easier and more principled.