A Consistent Estimator for Confounding Strength

Regression on observational data can fail to capture a causal relationship in the presence of unobserved confounding. Confounding strength measures this mismatch, but estimating it requires itself additional assumptions. A common assumption is the independence of causal mechanisms, which relies on concentration phenomena in high dimensions. While high dimensions enable the estimation of confounding strength, they also necessitate adapted estimators. In this paper, we derive the asymptotic behavior of the confounding strength estimator by Janzing and Sch\"olkopf (2018) and show that it is generally not consistent. We then use tools from random matrix theory to derive an adapted, consistent estimator.

Discovering Inductive Bias with Gibbs Priors: A Diagnostic Tool for Approximate Bayesian Inference

Full Bayesian posteriors are rarely analytically tractable, which is why real-world Bayesian inference heavily relies on approximate techniques. Approximations generally differ from the true posterior and require diagnostic tools to assess whether the inference can still be trusted. We investigate a new approach to diagnosing approximate inference: the approximation mismatch is attributed to a change in the inductive bias by treating the approximations as exact and reverse-engineering the corresponding prior. We show that the problem is more complicated than it appears to be at first glance, because the solution generally depends on the observation. By reframing the problem in terms of incompatible conditional distributions we arrive at a natural solution: the Gibbs prior. The resulting diagnostic is based on pseudo-Gibbs sampling, which is widely applicable and easy to implement. We illustrate how the Gibbs prior can be used to discover the inductive bias in a controlled Gaussian setting and for a variety of Bayesian models and approximations.

Interpolation and Regularization for Causal Learning

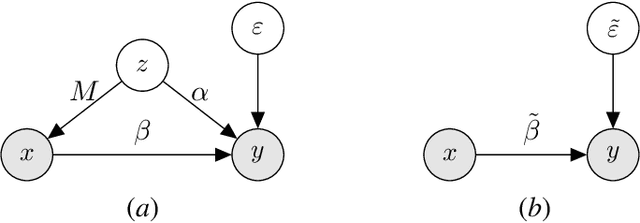
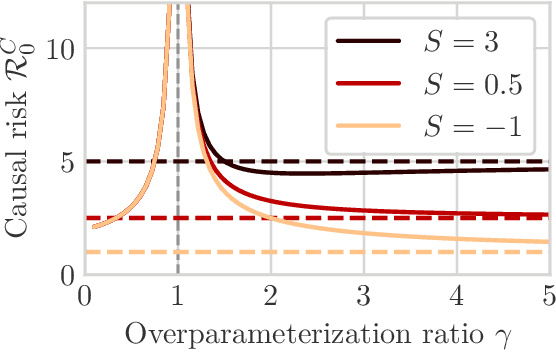
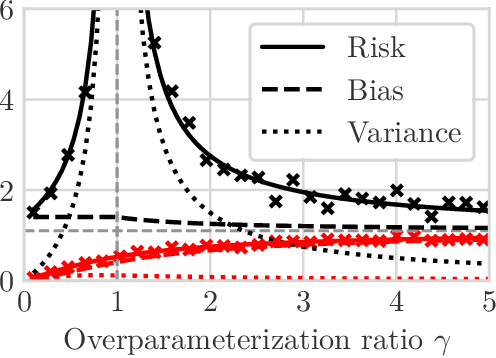
We study the problem of learning causal models from observational data through the lens of interpolation and its counterpart -- regularization. A large volume of recent theoretical, as well as empirical work, suggests that, in highly complex model classes, interpolating estimators can have good statistical generalization properties and can even be optimal for statistical learning. Motivated by an analogy between statistical and causal learning recently highlighted by Janzing (2019), we investigate whether interpolating estimators can also learn good causal models. To this end, we consider a simple linearly confounded model and derive precise asymptotics for the *causal risk* of the min-norm interpolator and ridge-regularized regressors in the high-dimensional regime. Under the principle of independent causal mechanisms, a standard assumption in causal learning, we find that interpolators cannot be optimal and causal learning requires stronger regularization than statistical learning. This resolves a recent conjecture in Janzing (2019). Beyond this assumption, we find a larger range of behavior that can be precisely characterized with a new measure of *confounding strength*. If the confounding strength is negative, causal learning requires weaker regularization than statistical learning, interpolators can be optimal, and the optimal regularization can even be negative. If the confounding strength is large, the optimal regularization is infinite, and learning from observational data is actively harmful.

Tangles: From Weak to Strong Clustering

We introduce a new approach to clustering by using tangles, a tool that originates in mathematical graph theory. Given a collection of "weak partitions" of a data set, tangles provide a framework to aggregate these weak partitions such that they "point in the direction of a cluster". As a result, a cluster is softly characterized by a set of consistent pointers. This mechanism provides a highly flexible way of solving soft clustering problems in a variety of setups, ranging from questionnaires over community detection in graphs to clustering points in metric spaces. Conceptually, tangles have many intriguing properties: (1) Similar to boosting, which combines many weak classifiers to a strong classifier, tangles provide a formal way to combine many weak partitions to obtain few strong clusters. (2) In terms of computational complexity, tangles allow us to use simple, fast algorithms to produce the weak partitions. The complexity of identifying the strong partitions is dominated by the number of weak partitions, not the number of data points, leading to an interesting trade-off between the two. (3) If the weak partitions are interpretable, so are the strong partitions induced by the tangles, resulting in one of the rare algorithms to produce interpretable clusters. (4) The output of tangles is of a hierarchical nature, inducing the notion of a soft dendrogram that can be helpful in data visualization.