A Consistent Estimator for Confounding Strength
Paper and Code
Nov 03, 2022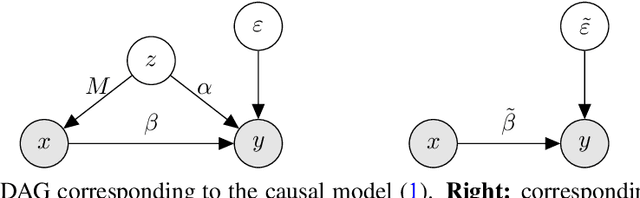
Regression on observational data can fail to capture a causal relationship in the presence of unobserved confounding. Confounding strength measures this mismatch, but estimating it requires itself additional assumptions. A common assumption is the independence of causal mechanisms, which relies on concentration phenomena in high dimensions. While high dimensions enable the estimation of confounding strength, they also necessitate adapted estimators. In this paper, we derive the asymptotic behavior of the confounding strength estimator by Janzing and Sch\"olkopf (2018) and show that it is generally not consistent. We then use tools from random matrix theory to derive an adapted, consistent estimator.
* 21 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge