Luca Dall'Asta
Inference in conditioned dynamics through causality restoration
Oct 18, 2022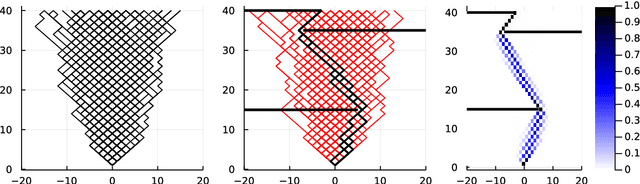
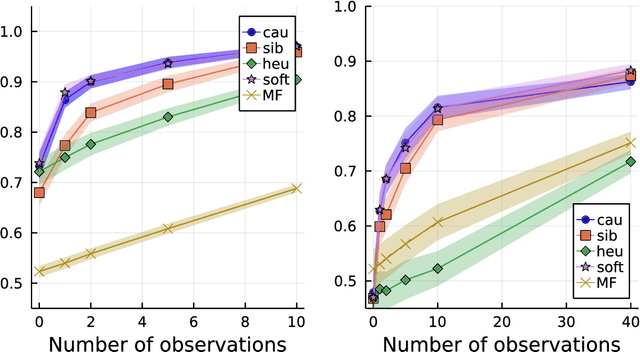
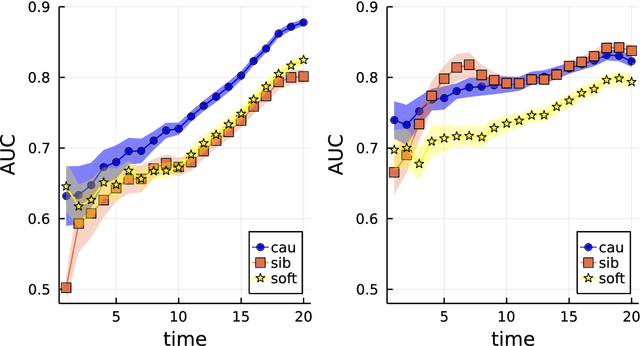
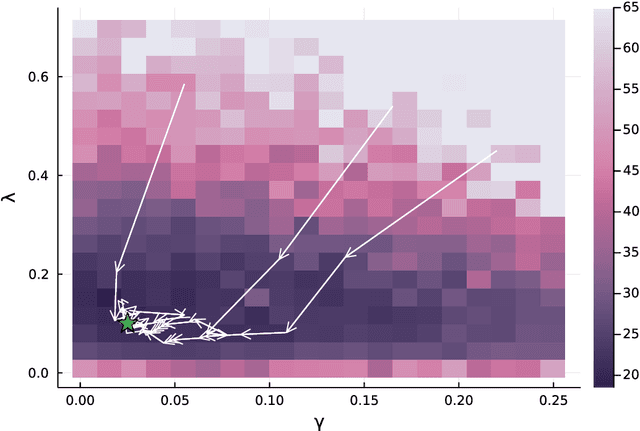
Abstract:Computing observables from conditioned dynamics is typically computationally hard, because, although obtaining independent samples efficiently from the unconditioned dynamics is usually feasible, generally most of the samples must be discarded (in a form of importance sampling) because they do not satisfy the imposed conditions. Sampling directly from the conditioned distribution is non-trivial, as conditioning breaks the causal properties of the dynamics which ultimately renders the sampling procedure efficient. One standard way of achieving it is through a Metropolis Monte-Carlo procedure, but this procedure is normally slow and a very large number of Monte-Carlo steps is needed to obtain a small number of statistically independent samples. In this work, we propose an alternative method to produce independent samples from a conditioned distribution. The method learns the parameters of a generalized dynamical model that optimally describe the conditioned distribution in a variational sense. The outcome is an effective, unconditioned, dynamical model, from which one can trivially obtain independent samples, effectively restoring causality of the conditioned distribution. The consequences are twofold: on the one hand, it allows us to efficiently compute observables from the conditioned dynamics by simply averaging over independent samples. On the other hand, the method gives an effective unconditioned distribution which is easier to interpret. The method is flexible and can be applied virtually to any dynamics. We discuss an important application of the method, namely the problem of epidemic risk assessment from (imperfect) clinical tests, for a large family of time-continuous epidemic models endowed with a Gillespie-like sampler. We show that the method compares favorably against the state of the art, including the soft-margin approach and mean-field methods.
Epidemic inference through generative neural networks
Nov 08, 2021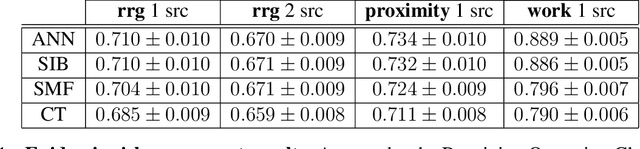


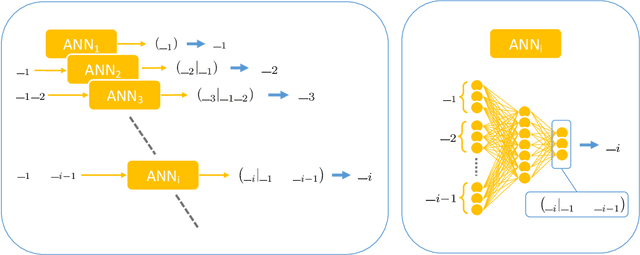
Abstract:Reconstructing missing information in epidemic spreading on contact networks can be essential in prevention and containment strategies. For instance, identifying and warning infective but asymptomatic individuals (e.g., manual contact tracing) helped contain outbreaks in the COVID-19 pandemic. The number of possible epidemic cascades typically grows exponentially with the number of individuals involved. The challenge posed by inference problems in the epidemics processes originates from the difficulty of identifying the almost negligible subset of those compatible with the evidence (for instance, medical tests). Here we present a new generative neural networks framework that can sample the most probable infection cascades compatible with observations. Moreover, the framework can infer the parameters governing the spreading of infections. The proposed method obtains better or comparable results with existing methods on the patient zero problem, risk assessment, and inference of infectious parameters in synthetic and real case scenarios like spreading infections in workplaces and hospitals.
Epidemic mitigation by statistical inference from contact tracing data
Sep 20, 2020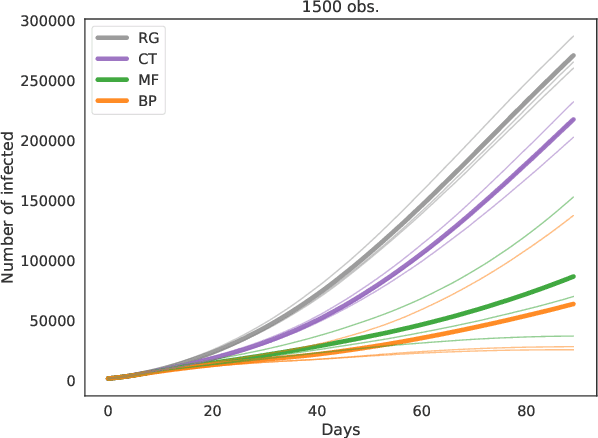
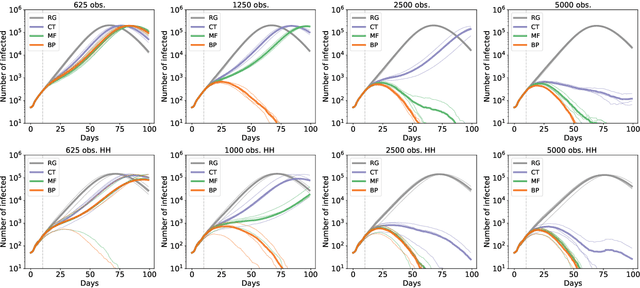
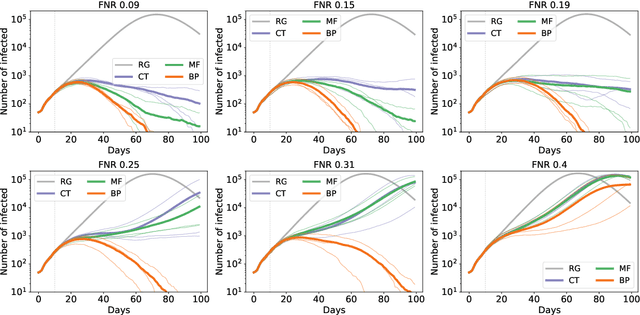

Abstract:Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.
Loop corrections in spin models through density consistency
Oct 24, 2018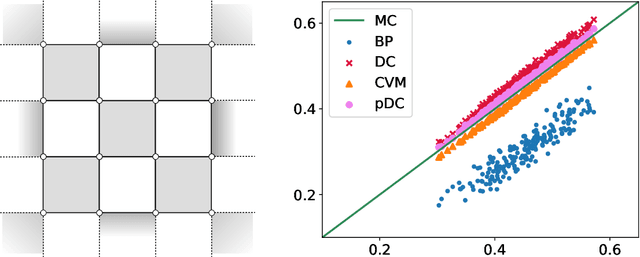
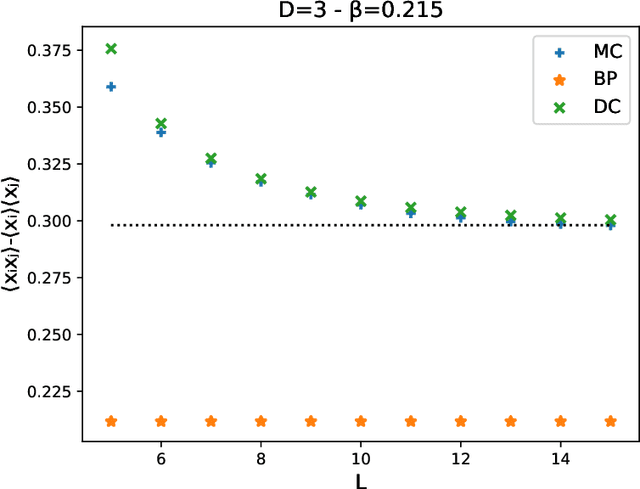
Abstract:Computing marginal distributions of discrete or semi-discrete Markov Random Fields (MRF) is a fundamental, generally intractable, problem with a vast number of applications on virtually all fields of science. We present a new family of computational schemes to calculate approximately marginals of discrete MRFs. This method shares some desirable properties with Belief Propagation, in particular providing exact marginals on acyclic graphs; but at difference with it, it includes some loop corrections, i.e. it takes into account correlations coming from all cycles in the factor graph. It is also similar to Adaptive TAP, but at difference with it, the consistency is not on the first two moments of the distribution but rather on the value of its density on a subset of values. Results on random connectivity and finite dimensional Ising and Edward-Anderson models show a significant improvement with respect to the Bethe-Peierls (tree) approximation in all cases, and significant improvement with respect to Cluster Variational Method and Loop Corrected Bethe approximation in many cases. In particular, for the critical inverse temperature $\beta_{c}$ of the homogeneous hypercubic lattice, the $1/d$ expansion of $\left(d\beta_{c}\right)^{-1}$ of the proposed scheme is exact up to the $d^{-3}$ order, whereas the two latter are exact only up to the $d^{-2}$ order.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge