Quantifying Behavioural Distance Between Mathematical Expressions

Existing symbolic regression methods organize the space of candidate mathematical expressions primarily based on their syntactic, structural similarity. However, this approach overlooks crucial equivalences between expressions that arise from mathematical symmetries, such as commutativity, associativity, and distribution laws for arithmetic operations. Consequently, expressions with similar errors on a given data set are apart from each other in the search space. This leads to a rough error landscape in the search space that efficient local, gradient-based methods cannot explore. This paper proposes and implements a measure of a behavioral distance, BED, that clusters together expressions with similar errors. The experimental results show that the stochastic method for calculating BED achieves consistency with a modest number of sampled values for evaluating the expressions. This leads to computational efficiency comparable to the tree-based syntactic distance. Our findings also reveal that BED significantly improves the smoothness of the error landscape in the search space for symbolic regression.

MLFMF: Data Sets for Machine Learning for Mathematical Formalization

We introduce MLFMF, a collection of data sets for benchmarking recommendation systems used to support formalization of mathematics with proof assistants. These systems help humans identify which previous entries (theorems, constructions, datatypes, and postulates) are relevant in proving a new theorem or carrying out a new construction. Each data set is derived from a library of formalized mathematics written in proof assistants Agda or Lean. The collection includes the largest Lean~4 library Mathlib, and some of the largest Agda libraries: the standard library, the library of univalent mathematics Agda-unimath, and the TypeTopology library. Each data set represents the corresponding library in two ways: as a heterogeneous network, and as a list of s-expressions representing the syntax trees of all the entries in the library. The network contains the (modular) structure of the library and the references between entries, while the s-expressions give complete and easily parsed information about every entry. We report baseline results using standard graph and word embeddings, tree ensembles, and instance-based learning algorithms. The MLFMF data sets provide solid benchmarking support for further investigation of the numerous machine learning approaches to formalized mathematics. The methodology used to extract the networks and the s-expressions readily applies to other libraries, and is applicable to other proof assistants. With more than $250\,000$ entries in total, this is currently the largest collection of formalized mathematical knowledge in machine learnable format.

Efficient Generator of Mathematical Expressions for Symbolic Regression

We propose an approach to symbolic regression based on a novel variational autoencoder for generating hierarchical structures, HVAE. It combines simple atomic units with shared weights to recursively encode and decode the individual nodes in the hierarchy. Encoding is performed bottom-up and decoding top-down. We empirically show that HVAE can be trained efficiently with small corpora of mathematical expressions and can accurately encode expressions into a smooth low-dimensional latent space. The latter can be efficiently explored with various optimization methods to address the task of symbolic regression. Indeed, random search through the latent space of HVAE performs better than random search through expressions generated by manually crafted probabilistic grammars for mathematical expressions. Finally, EDHiE system for symbolic regression, which applies an evolutionary algorithm to the latent space of HVAE, reconstructs equations from a standard symbolic regression benchmark better than a state-of-the-art system based on a similar combination of deep learning and evolutionary algorithms.\v{z}

P(Expression

Probabilistic context-free grammars have a long-term record of use as generative models in machine learning and symbolic regression. When used for symbolic regression, they generate algebraic expressions. We define the latter as equivalence classes of strings derived by grammar and address the problem of calculating the probability of deriving a given expression with a given grammar. We show that the problem is undecidable in general. We then present specific grammars for generating linear, polynomial, and rational expressions, where algorithms for calculating the probability of a given expression exist. For those grammars, we design algorithms for calculating the exact probability and efficient approximation with arbitrary precision.

Boosting the Performance of Quantum Annealers using Machine Learning

Noisy intermediate-scale quantum (NISQ) devices are spearheading the second quantum revolution. Of these, quantum annealers are the only ones currently offering real world, commercial applications on as many as 5000 qubits. The size of problems that can be solved by quantum annealers is limited mainly by errors caused by environmental noise and intrinsic imperfections of the processor. We address the issue of intrinsic imperfections with a novel error correction approach, based on machine learning methods. Our approach adjusts the input Hamiltonian to maximize the probability of finding the solution. In our experiments, the proposed error correction method improved the performance of annealing by up to three orders of magnitude and enabled the solving of a previously intractable, maximally complex problem.

Explaining the Performance of Multi-label Classification Methods with Data Set Properties

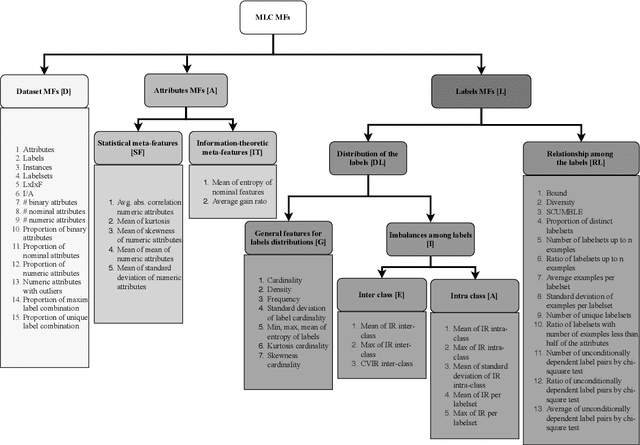
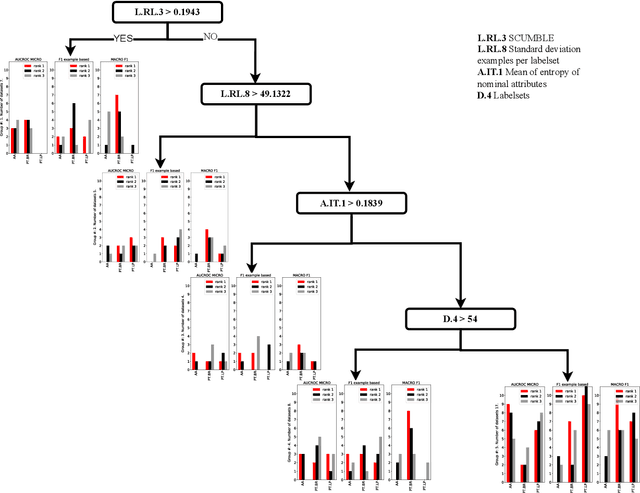
Meta learning generalizes the empirical experience with different learning tasks and holds promise for providing important empirical insight into the behaviour of machine learning algorithms. In this paper, we present a comprehensive meta-learning study of data sets and methods for multi-label classification (MLC). MLC is a practically relevant machine learning task where each example is labelled with multiple labels simultaneously. Here, we analyze 40 MLC data sets by using 50 meta features describing different properties of the data. The main findings of this study are as follows. First, the most prominent meta features that describe the space of MLC data sets are the ones assessing different aspects of the label space. Second, the meta models show that the most important meta features describe the label space, and, the meta features describing the relationships among the labels tend to occur a bit more often than the meta features describing the distributions between and within the individual labels. Third, the optimization of the hyperparameters can improve the predictive performance, however, quite often the extent of the improvements does not always justify the resource utilization.

Comprehensive Comparative Study of Multi-Label Classification Methods

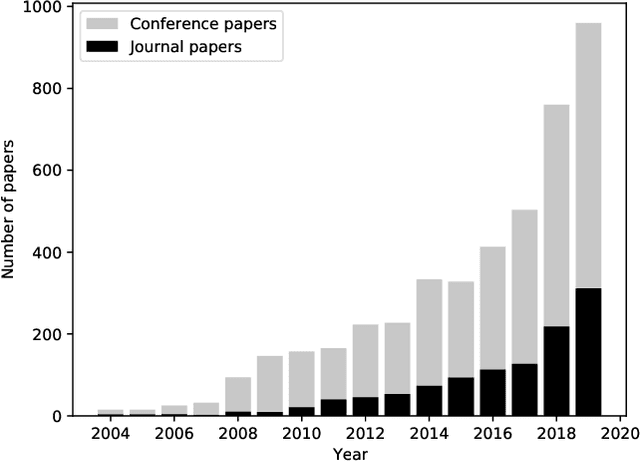
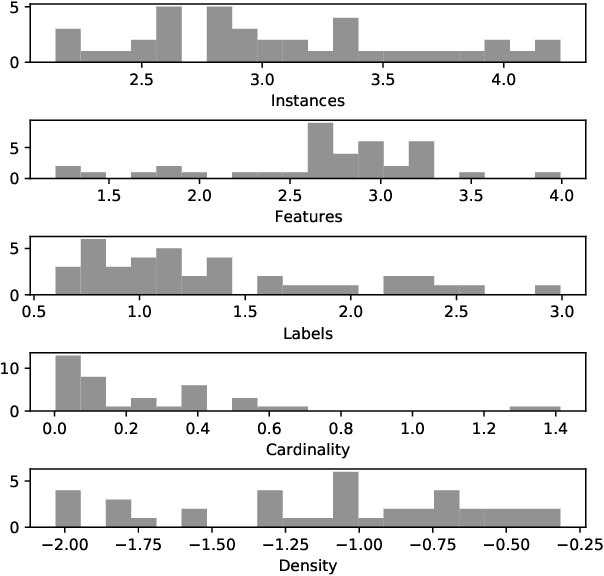
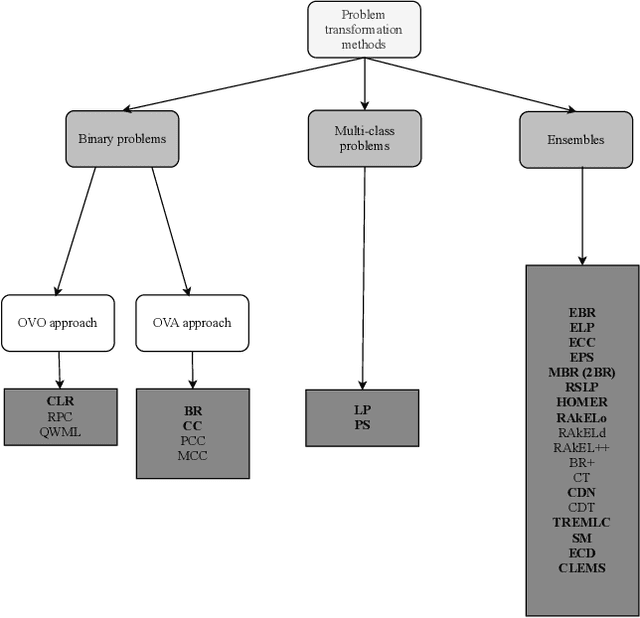
Multi-label classification (MLC) has recently received increasing interest from the machine learning community. Several studies provide reviews of methods and datasets for MLC and a few provide empirical comparisons of MLC methods. However, they are limited in the number of methods and datasets considered. This work provides a comprehensive empirical study of a wide range of MLC methods on a plethora of datasets from various domains. More specifically, our study evaluates 26 methods on 42 benchmark datasets using 20 evaluation measures. The adopted evaluation methodology adheres to the highest literature standards for designing and executing large scale, time-budgeted experimental studies. First, the methods are selected based on their usage by the community, assuring representation of methods across the MLC taxonomy of methods and different base learners. Second, the datasets cover a wide range of complexity and domains of application. The selected evaluation measures assess the predictive performance and the efficiency of the methods. The results of the analysis identify RFPCT, RFDTBR, ECCJ48, EBRJ48 and AdaBoostMH as best performing methods across the spectrum of performance measures. Whenever a new method is introduced, it should be compared to different subsets of MLC methods, determined on the basis of the different evaluation criteria.

Probabilistic Grammars for Equation Discovery

Equation discovery, also known as symbolic regression, is a type of automated modeling that discovers scientific laws, expressed in the form of equations, from observed data and expert knowledge. Deterministic grammars, such as context-free grammars, have been used to limit the search spaces in equation discovery by providing hard constraints that specify which equations to consider and which not. In this paper, we propose the use of probabilistic context-free grammars in the context of equation discovery. Such grammars encode soft constraints on the space of equations, specifying a prior probability distribution on the space of possible equations. We show that probabilistic grammars can be used to elegantly and flexibly formulate the parsimony principle, that favors simpler equations, through probabilities attached to the rules in the grammars. We demonstrate that the use of probabilistic, rather than deterministic grammars, in the context of a Monte-Carlo algorithm for grammar-based equation discovery, leads to more efficient equation discovery. Finally, by specifying prior probability distributions over equation spaces, the foundations are laid for Bayesian approaches to equation discovery.

Equation Discovery for Nonlinear System Identification

Equation discovery methods enable modelers to combine domain-specific knowledge and system identification to construct models most suitable for a selected modeling task. The method described and evaluated in this paper can be used as a nonlinear system identification method for gray-box modeling. It consists of two interlaced parts of modeling that are computer-aided. The first performs computer-aided identification of a model structure composed of elements selected from user-specified domain-specific modeling knowledge, while the second part performs parameter estimation. In this paper, recent developments of the equation discovery method called process-based modeling, suited for nonlinear system identification, are elaborated and illustrated on two continuous-time case studies. The first case study illustrates the use of the process-based modeling on synthetic data while the second case-study evaluates on measured data for a standard system-identification benchmark. The experimental results clearly demonstrate the ability of process-based modeling to reconstruct both model structure and parameters from measured data.

Meta-Model Framework for Surrogate-Based Parameter Estimation in Dynamical Systems

The central task in modeling complex dynamical systems is parameter estimation. This task involves numerous evaluations of a computationally expensive objective function. Surrogate-based optimization introduces a computationally efficient predictive model that approximates the value of the objective function. The standard approach involves learning a surrogate from training examples that correspond to past evaluations of the objective function. Current surrogate-based optimization methods use static, predefined substitution strategies that decide when to use the surrogate and when the true objective. We introduce a meta-model framework where the substitution strategy is dynamically adapted to the solution space of the given optimization problem. The meta model encapsulates the objective function, the surrogate model and the model of the substitution strategy, as well as components for learning them. The framework can be seamlessly coupled with an arbitrary optimization algorithm without any modification: it replaces the objective function and autonomously decides how to evaluate a given candidate solution. We test the utility of the framework on three tasks of estimating parameters of real-world models of dynamical systems. The results show that the meta model significantly improves the efficiency of optimization, reducing the total number of evaluations of the objective function up to an average of 77%.