Universal Fine-Grained Symmetry Inference and Enforcement for Rigorous Crystal Structure Prediction

Crystal structure prediction (CSP), which aims to predict the three-dimensional atomic arrangement of a crystal from its composition, is central to materials discovery and mechanistic understanding. Existing deep learning models often treat crystallographic symmetry only as a soft heuristic or rely on space group and Wyckoff templates retrieved from known structures, which limits both physical fidelity and the ability to discover genuinely new material structures. In contrast to retrieval-based methods, our approach leverages large language models to encode chemical semantics and directly generate fine-grained Wyckoff patterns from composition, effectively circumventing the limitations inherent to database lookups. Crucially, we incorporate domain knowledge into the generative process through an efficient constrained-optimization search that rigorously enforces algebraic consistency between site multiplicities and atomic stoichiometry. By integrating this symmetry-consistent template into a diffusion backbone, our approach constrains the stochastic generative trajectory to a physically valid geometric manifold. This framework achieves state-of-the-art performance across stability, uniqueness, and novelty (SUN) benchmarks, alongside superior matching performance, thereby establishing a new paradigm for the rigorous exploration of targeted crystallographic space. This framework enables efficient expansion into previously uncharted materials space, eliminating reliance on existing databases or a priori structural knowledge.

Constructing Invariant and Equivariant Operations by Symmetric Tensor Network

Design of neural networks that incorporate symmetry is crucial for geometric deep learning. Central to this effort is the development of invariant and equivariant operations. This works presents a systematic method for constructing valid invariant and equivariant operations. It can handle inputs and outputs in the form of Cartesian tensors with different rank, as well as spherical tensors with different types. In addition, our method features a graphical representation utilizing the symmetric tensor network, which simplifies both the proofs and constructions related to invariant and equivariant functions. We also apply this approach to design the equivariant interaction message for the geometry graph neural network, and equivariant machine learning model to learn the constitutive law of materials.

A Framework of SO-equivariant Non-linear Representation Learning and its Application to Electronic-Structure Hamiltonian Prediction

We present both a theoretical and a methodological framework that addresses a critical challenge in applying deep learning to physical systems: the reconciliation of non-linear expressiveness with SO(3)-equivariance in predictions of SO(3)-equivariant quantities, such as the electronic-structure Hamiltonian. Inspired by covariant theory in physics, we address this problem by exploring the mathematical relationships between SO(3)-invariant and SO(3)-equivariant quantities and their representations. We first construct theoretical SO(3)-invariant quantities derived from the SO(3)-equivariant regression targets, and use these invariant quantities as supervisory labels to guide the learning of high-quality SO(3)-invariant features. Given that SO(3)-invariance is preserved under non-linear operations, the encoding process for invariant features can extensively utilize non-linear mappings, thereby fully capturing the non-linear patterns inherent in physical systems. Building on this foundation, we propose a gradient-based mechanism to induce SO(3)-equivariant encodings of various degrees from the learned SO(3)-invariant features. This mechanism can incorporate non-linear expressive capabilities into SO(3)-equivariant representations, while theoretically preserving their equivariant properties as we prove. Our approach offers a promising general solution to the critical dilemma between equivariance and non-linear expressiveness in deep learning methodologies. We apply our theory and method to the electronic-structure Hamiltonian prediction tasks, demonstrating state-of-the-art performance across six benchmark databases.

Harmonizing Covariance and Expressiveness for Deep Hamiltonian Regression in Crystalline Material Research: a Hybrid Cascaded Regression Framework

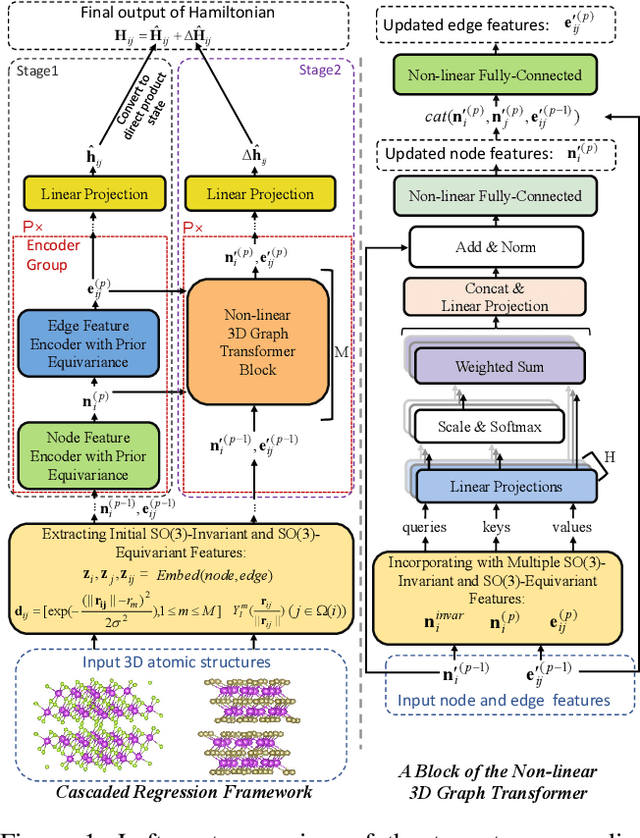
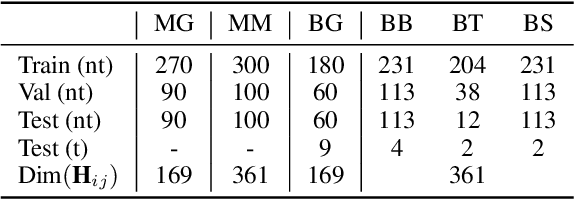
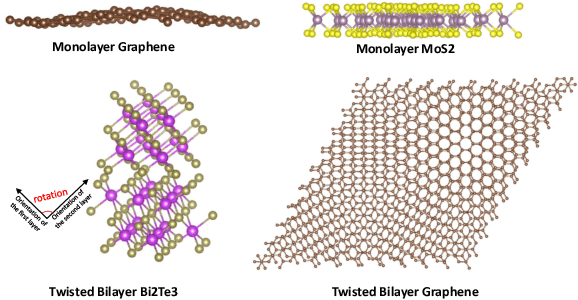
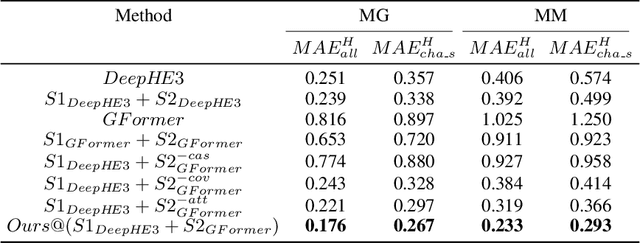
Deep learning for Hamiltonian regression of quantum systems in material research necessitates satisfying the covariance laws, among which achieving SO(3)-equivariance without sacrificing the expressiveness capability of networks remains an elusive challenge due to the restriction to non-linear mappings on guaranteeing theoretical equivariance. To alleviate the covariance-expressiveness dilemma, we propose a hybrid framework with two cascaded regression stages. The first stage, i.e., a theoretically-guaranteed covariant neural network modeling symmetry properties of 3D atom systems, predicts baseline Hamiltonians with theoretically covariant features extracted, assisting the second stage in learning covariance. Meanwhile, the second stage, powered by a non-linear 3D graph Transformer network we propose for structural modeling of atomic systems, refines the first stage's output as a fine-grained prediction of Hamiltonians with better expressiveness capability. The combination of a theoretically covariant yet inevitably less expressive model with a highly expressive non-linear network enables precise, generalizable predictions while maintaining robust covariance under coordinate transformations. Our method achieves state-of-the-art performance in Hamiltonian prediction for electronic structure calculations, confirmed through experiments on six crystalline material databases. The codes and configuration scripts are available in the supplementary material.

Molecular Property Prediction: A Multilevel Quantum Interactions Modeling Perspective

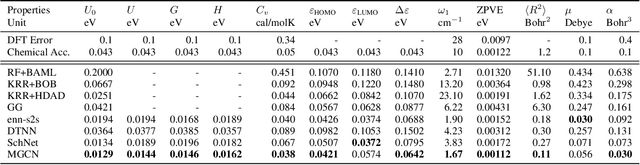
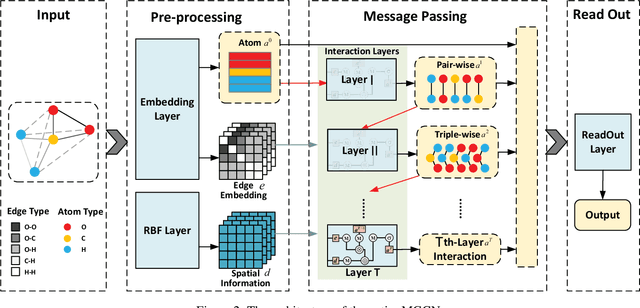
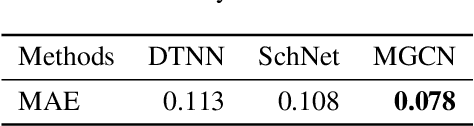
Predicting molecular properties (e.g., atomization energy) is an essential issue in quantum chemistry, which could speed up much research progress, such as drug designing and substance discovery. Traditional studies based on density functional theory (DFT) in physics are proved to be time-consuming for predicting large number of molecules. Recently, the machine learning methods, which consider much rule-based information, have also shown potentials for this issue. However, the complex inherent quantum interactions of molecules are still largely underexplored by existing solutions. In this paper, we propose a generalizable and transferable Multilevel Graph Convolutional neural Network (MGCN) for molecular property prediction. Specifically, we represent each molecule as a graph to preserve its internal structure. Moreover, the well-designed hierarchical graph neural network directly extracts features from the conformation and spatial information followed by the multilevel interactions. As a consequence, the multilevel overall representations can be utilized to make the prediction. Extensive experiments on both datasets of equilibrium and off-equilibrium molecules demonstrate the effectiveness of our model. Furthermore, the detailed results also prove that MGCN is generalizable and transferable for the prediction.