A Framework of SO-equivariant Non-linear Representation Learning and its Application to Electronic-Structure Hamiltonian Prediction

We present both a theoretical and a methodological framework that addresses a critical challenge in applying deep learning to physical systems: the reconciliation of non-linear expressiveness with SO(3)-equivariance in predictions of SO(3)-equivariant quantities, such as the electronic-structure Hamiltonian. Inspired by covariant theory in physics, we address this problem by exploring the mathematical relationships between SO(3)-invariant and SO(3)-equivariant quantities and their representations. We first construct theoretical SO(3)-invariant quantities derived from the SO(3)-equivariant regression targets, and use these invariant quantities as supervisory labels to guide the learning of high-quality SO(3)-invariant features. Given that SO(3)-invariance is preserved under non-linear operations, the encoding process for invariant features can extensively utilize non-linear mappings, thereby fully capturing the non-linear patterns inherent in physical systems. Building on this foundation, we propose a gradient-based mechanism to induce SO(3)-equivariant encodings of various degrees from the learned SO(3)-invariant features. This mechanism can incorporate non-linear expressive capabilities into SO(3)-equivariant representations, while theoretically preserving their equivariant properties as we prove. Our approach offers a promising general solution to the critical dilemma between equivariance and non-linear expressiveness in deep learning methodologies. We apply our theory and method to the electronic-structure Hamiltonian prediction tasks, demonstrating state-of-the-art performance across six benchmark databases.

Harmonizing Covariance and Expressiveness for Deep Hamiltonian Regression in Crystalline Material Research: a Hybrid Cascaded Regression Framework

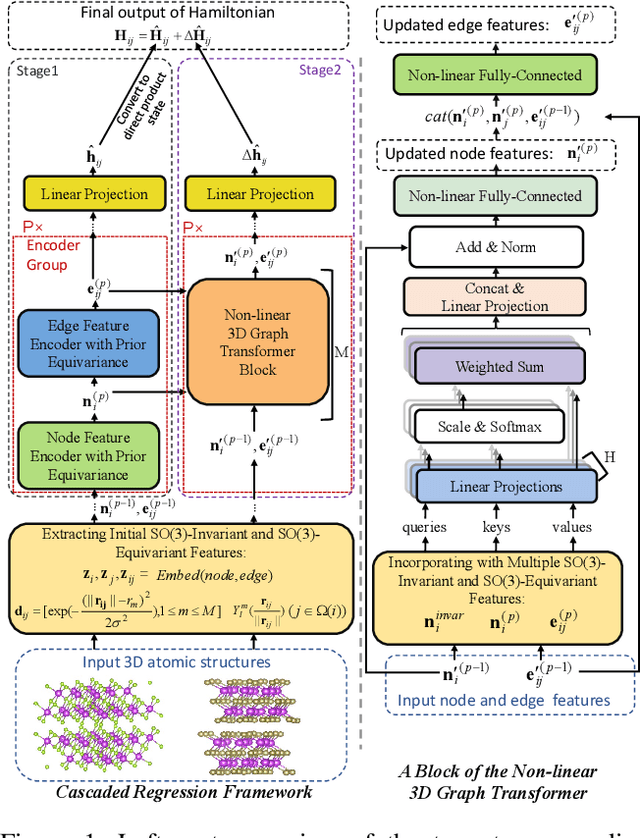
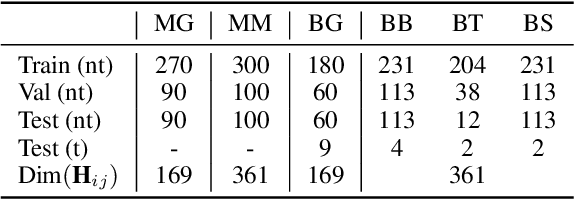
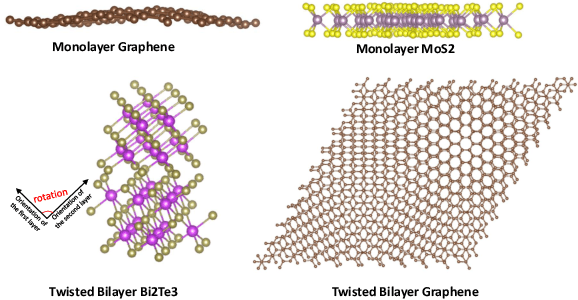
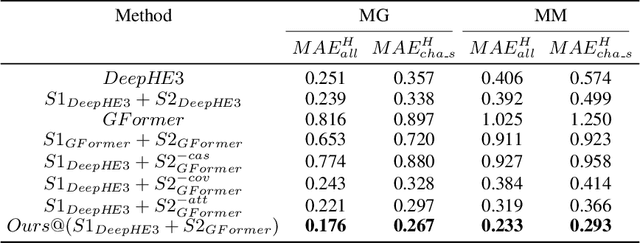
Deep learning for Hamiltonian regression of quantum systems in material research necessitates satisfying the covariance laws, among which achieving SO(3)-equivariance without sacrificing the expressiveness capability of networks remains an elusive challenge due to the restriction to non-linear mappings on guaranteeing theoretical equivariance. To alleviate the covariance-expressiveness dilemma, we propose a hybrid framework with two cascaded regression stages. The first stage, i.e., a theoretically-guaranteed covariant neural network modeling symmetry properties of 3D atom systems, predicts baseline Hamiltonians with theoretically covariant features extracted, assisting the second stage in learning covariance. Meanwhile, the second stage, powered by a non-linear 3D graph Transformer network we propose for structural modeling of atomic systems, refines the first stage's output as a fine-grained prediction of Hamiltonians with better expressiveness capability. The combination of a theoretically covariant yet inevitably less expressive model with a highly expressive non-linear network enables precise, generalizable predictions while maintaining robust covariance under coordinate transformations. Our method achieves state-of-the-art performance in Hamiltonian prediction for electronic structure calculations, confirmed through experiments on six crystalline material databases. The codes and configuration scripts are available in the supplementary material.