Harmonizing Covariance and Expressiveness for Deep Hamiltonian Regression in Crystalline Material Research: a Hybrid Cascaded Regression Framework
Paper and Code
Jan 15, 2024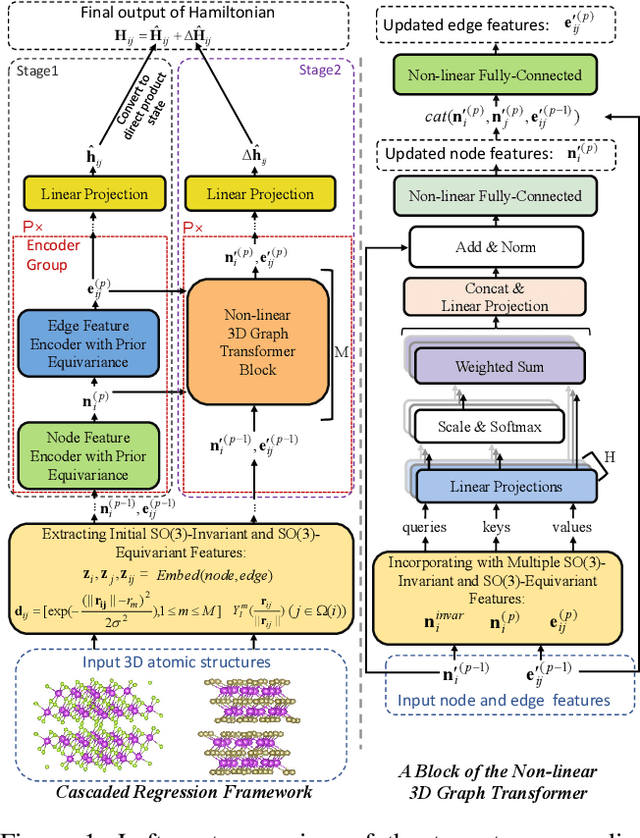
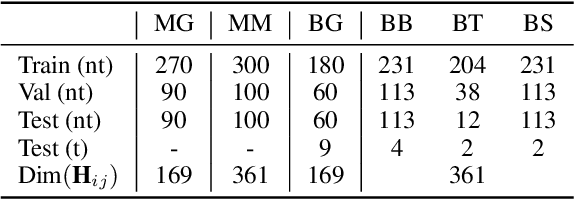
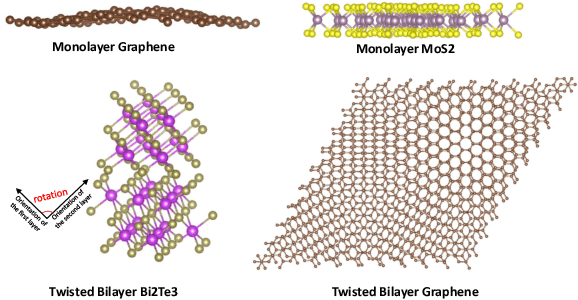
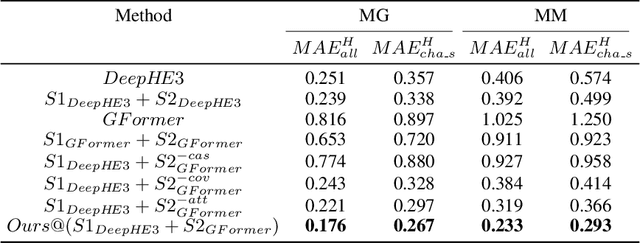
Deep learning for Hamiltonian regression of quantum systems in material research necessitates satisfying the covariance laws, among which achieving SO(3)-equivariance without sacrificing the expressiveness capability of networks remains an elusive challenge due to the restriction to non-linear mappings on guaranteeing theoretical equivariance. To alleviate the covariance-expressiveness dilemma, we propose a hybrid framework with two cascaded regression stages. The first stage, i.e., a theoretically-guaranteed covariant neural network modeling symmetry properties of 3D atom systems, predicts baseline Hamiltonians with theoretically covariant features extracted, assisting the second stage in learning covariance. Meanwhile, the second stage, powered by a non-linear 3D graph Transformer network we propose for structural modeling of atomic systems, refines the first stage's output as a fine-grained prediction of Hamiltonians with better expressiveness capability. The combination of a theoretically covariant yet inevitably less expressive model with a highly expressive non-linear network enables precise, generalizable predictions while maintaining robust covariance under coordinate transformations. Our method achieves state-of-the-art performance in Hamiltonian prediction for electronic structure calculations, confirmed through experiments on six crystalline material databases. The codes and configuration scripts are available in the supplementary material.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge