Memory-Efficient Factorization Machines via Binarizing both Data and Model Coefficients

Factorization Machines (FM), a general predictor that can efficiently model feature interactions in linear time, was primarily proposed for collaborative recommendation and have been broadly used for regression, classification and ranking tasks. Subspace Encoding Factorization Machine (SEFM) has been proposed recently to overcome the expressiveness limitation of Factorization Machines (FM) by applying explicit nonlinear feature mapping for both individual features and feature interactions through one-hot encoding to each input feature. Despite the effectiveness of SEFM, it increases the memory cost of FM by $b$ times, where $b$ is the number of bins when applying one-hot encoding on each input feature. To reduce the memory cost of SEFM, we propose a new method called Binarized FM which constraints the model parameters to be binary values (i.e., 1 or $-1$). Then each parameter value can be efficiently stored in one bit. Our proposed method can significantly reduce the memory cost of SEFM model. In addition, we propose a new algorithm to effectively and efficiently learn proposed FM with binary constraints using Straight Through Estimator (STE) with Adaptive Gradient Descent (Adagrad). Finally, we evaluate the performance of our proposed method on eight different classification datasets. Our experimental results have demonstrated that our proposed method achieves comparable accuracy with SEFM but with much less memory cost.

Effective and Sparse Count-Sketch via k-means clustering

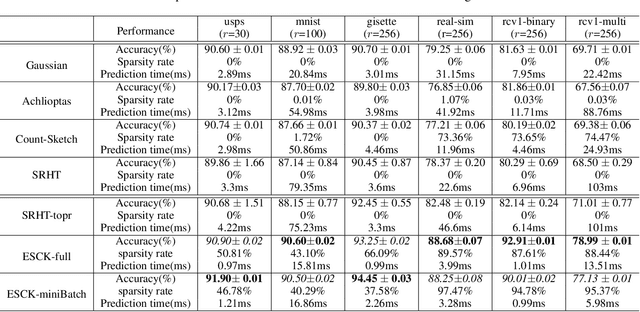
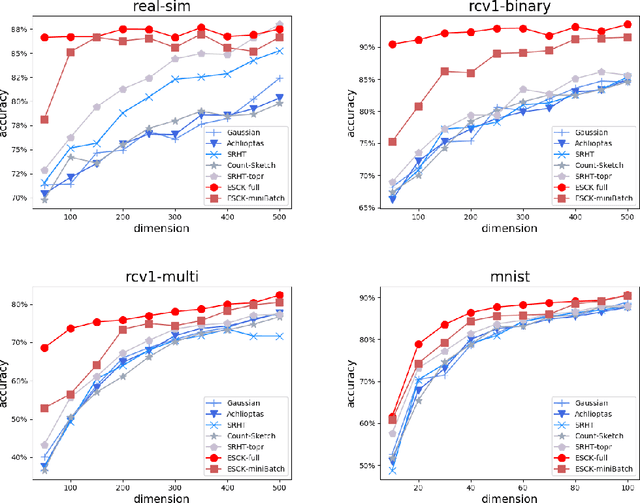
Count-sketch is a popular matrix sketching algorithm that can produce a sketch of an input data matrix X in O(nnz(X))time where nnz(X) denotes the number of non-zero entries in X. The sketched matrix will be much smaller than X while preserving most of its properties. Therefore, count-sketch is widely used for addressing high-dimensionality challenge in machine learning. However, there are two main limitations of count-sketch: (1) The sketching matrix used count-sketch is generated randomly which does not consider any intrinsic data properties of X. This data-oblivious matrix sketching method could produce a bad sketched matrix which will result in low accuracy for subsequent machine learning tasks (e.g.classification); (2) For highly sparse input data, count-sketch could produce a dense sketched data matrix. This dense sketch matrix could make the subsequent machine learning tasks more computationally expensive than on the original sparse data X. To address these two limitations, we first show an interesting connection between count-sketch and k-means clustering by analyzing the reconstruction error of the count-sketch method. Based on our analysis, we propose to reduce the reconstruction error of count-sketch by using k-means clustering algorithm to obtain the low-dimensional sketched matrix. In addition, we propose to solve k-mean clustering using gradient descent with -L1 ball projection to produce a sparse sketched matrix. Our experimental results based on six real-life classification datasets have demonstrated that our proposed method achieves higher accuracy than the original count-sketch and other popular matrix sketching algorithms. Our results also demonstrate that our method produces a sparser sketched data matrix than other methods and therefore the prediction cost of our method will be smaller than other matrix sketching methods.

Compressing Deep Convolutional Neural Networks by Stacking Low-dimensional Binary Convolution Filters

Deep Convolutional Neural Networks (CNN) have been successfully applied to many real-life problems. However, the huge memory cost of deep CNN models poses a great challenge of deploying them on memory-constrained devices (e.g., mobile phones). One popular way to reduce the memory cost of deep CNN model is to train binary CNN where the weights in convolution filters are either 1 or -1 and therefore each weight can be efficiently stored using a single bit. However, the compression ratio of existing binary CNN models is upper bounded by around 32. To address this limitation, we propose a novel method to compress deep CNN model by stacking low-dimensional binary convolution filters. Our proposed method approximates a standard convolution filter by selecting and stacking filters from a set of low-dimensional binary convolution filters. This set of low-dimensional binary convolution filters is shared across all filters for a given convolution layer. Therefore, our method will achieve much larger compression ratio than binary CNN models. In order to train our proposed model, we have theoretically shown that our proposed model is equivalent to select and stack intermediate feature maps generated by low-dimensional binary filters. Therefore, our proposed model can be efficiently trained using the split-transform-merge strategy. We also provide detailed analysis of the memory and computation cost of our model in model inference. We compared the proposed method with other five popular model compression techniques on two benchmark datasets. Our experimental results have demonstrated that our proposed method achieves much higher compression ratio than existing methods while maintains comparable accuracy.

Memory and Computation-Efficient Kernel SVM via Binary Embedding and Ternary Model Coefficients

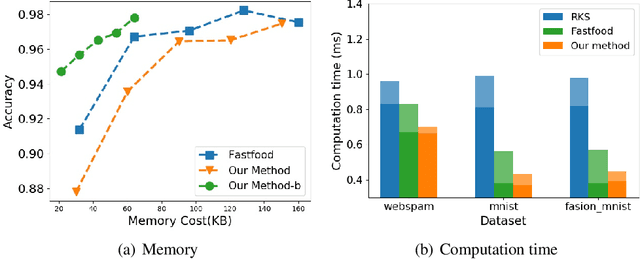
Kernel approximation is widely used to scale up kernel SVM training and prediction. However, the memory and computation costs of kernel approximation models are still too high if we want to deploy them on memory-limited devices such as mobile phones, smartwatches, and IoT devices. To address this challenge, we propose a novel memory and computation-efficient kernel SVM model by using both binary embedding and binary model coefficients. First, we propose an efficient way to generate compact binary embedding of the data, preserving the kernel similarity. Second, we propose a simple but effective algorithm to learn a linear classification model with ternary coefficients that can support different types of loss function and regularizer. Our algorithm can achieve better generalization accuracy than existing works on learning binary coefficients since we allow coefficient to be $-1$, $0$, or $1$ during the training stage, and coefficient $0$ can be removed during model inference for binary classification. Moreover, we provide a detailed analysis of the convergence of our algorithm and the inference complexity of our model. The analysis shows that the convergence to a local optimum is guaranteed, and the inference complexity of our model is much lower than other competing methods. Our experimental results on five large real-world datasets have demonstrated that our proposed method can build accurate nonlinear SVM models with memory costs less than 30KB.

Improved Subsampled Randomized Hadamard Transform for Linear SVM

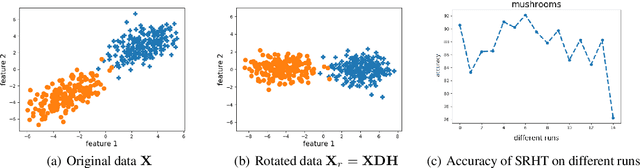
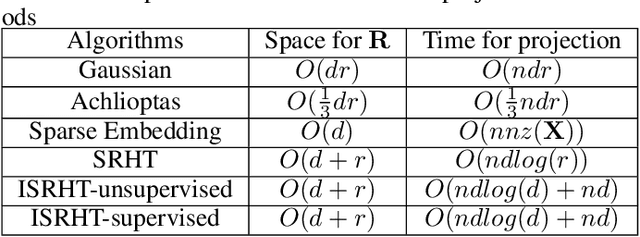
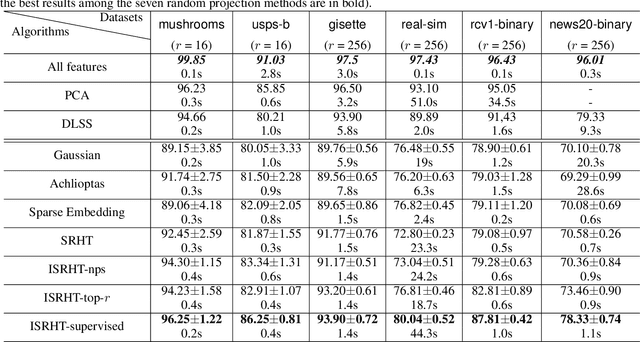
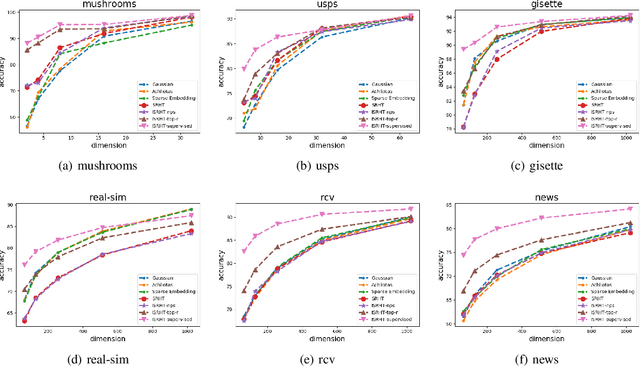
Subsampled Randomized Hadamard Transform (SRHT), a popular random projection method that can efficiently project a $d$-dimensional data into $r$-dimensional space ($r \ll d$) in $O(dlog(d))$ time, has been widely used to address the challenge of high-dimensionality in machine learning. SRHT works by rotating the input data matrix $\mathbf{X} \in \mathbb{R}^{n \times d}$ by Randomized Walsh-Hadamard Transform followed with a subsequent uniform column sampling on the rotated matrix. Despite the advantages of SRHT, one limitation of SRHT is that it generates the new low-dimensional embedding without considering any specific properties of a given dataset. Therefore, this data-independent random projection method may result in inferior and unstable performance when used for a particular machine learning task, e.g., classification. To overcome this limitation, we analyze the effect of using SRHT for random projection in the context of linear SVM classification. Based on our analysis, we propose importance sampling and deterministic top-$r$ sampling to produce effective low-dimensional embedding instead of uniform sampling SRHT. In addition, we also proposed a new supervised non-uniform sampling method. Our experimental results have demonstrated that our proposed methods can achieve higher classification accuracies than SRHT and other random projection methods on six real-life datasets.

Inductive Kernel Low-rank Decomposition with Priors: A Generalized Nystrom Method

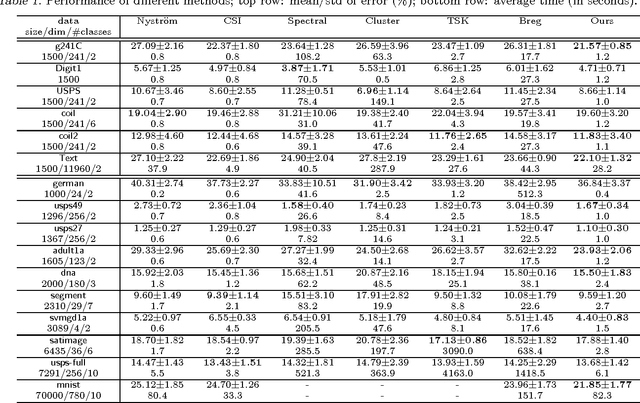
Low-rank matrix decomposition has gained great popularity recently in scaling up kernel methods to large amounts of data. However, some limitations could prevent them from working effectively in certain domains. For example, many existing approaches are intrinsically unsupervised, which does not incorporate side information (e.g., class labels) to produce task specific decompositions; also, they typically work "transductively", i.e., the factorization does not generalize to new samples, so the complete factorization needs to be recomputed when new samples become available. To solve these problems, in this paper we propose an"inductive"-flavored method for low-rank kernel decomposition with priors. We achieve this by generalizing the Nystr\"om method in a novel way. On the one hand, our approach employs a highly flexible, nonparametric structure that allows us to generalize the low-rank factors to arbitrarily new samples; on the other hand, it has linear time and space complexities, which can be orders of magnitudes faster than existing approaches and renders great efficiency in learning a low-rank kernel decomposition. Empirical results demonstrate the efficacy and efficiency of the proposed method.