Fair Effect Attribution in Parallel Online Experiments

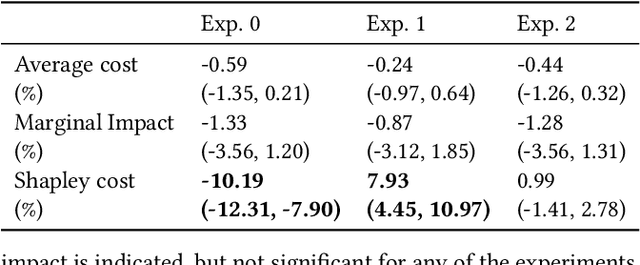
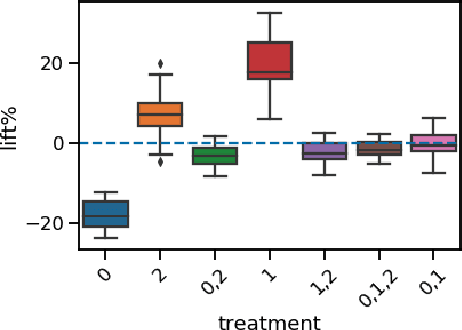
A/B tests serve the purpose of reliably identifying the effect of changes introduced in online services. It is common for online platforms to run a large number of simultaneous experiments by splitting incoming user traffic randomly in treatment and control groups. Despite a perfect randomization between different groups, simultaneous experiments can interact with each other and create a negative impact on average population outcomes such as engagement metrics. These are measured globally and monitored to protect overall user experience. Therefore, it is crucial to measure these interaction effects and attribute their overall impact in a fair way to the respective experimenters. We suggest an approach to measure and disentangle the effect of simultaneous experiments by providing a cost sharing approach based on Shapley values. We also provide a counterfactual perspective, that predicts shared impact based on conditional average treatment effects making use of causal inference techniques. We illustrate our approach in real world and synthetic data experiments.

Inductive Kernel Low-rank Decomposition with Priors: A Generalized Nystrom Method

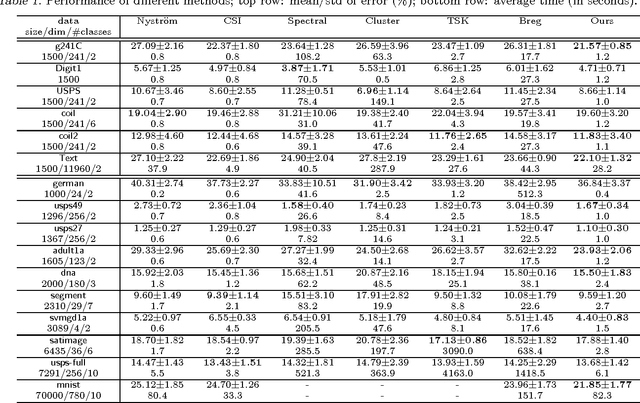
Low-rank matrix decomposition has gained great popularity recently in scaling up kernel methods to large amounts of data. However, some limitations could prevent them from working effectively in certain domains. For example, many existing approaches are intrinsically unsupervised, which does not incorporate side information (e.g., class labels) to produce task specific decompositions; also, they typically work "transductively", i.e., the factorization does not generalize to new samples, so the complete factorization needs to be recomputed when new samples become available. To solve these problems, in this paper we propose an"inductive"-flavored method for low-rank kernel decomposition with priors. We achieve this by generalizing the Nystr\"om method in a novel way. On the one hand, our approach employs a highly flexible, nonparametric structure that allows us to generalize the low-rank factors to arbitrarily new samples; on the other hand, it has linear time and space complexities, which can be orders of magnitudes faster than existing approaches and renders great efficiency in learning a low-rank kernel decomposition. Empirical results demonstrate the efficacy and efficiency of the proposed method.