Effective and Sparse Count-Sketch via k-means clustering

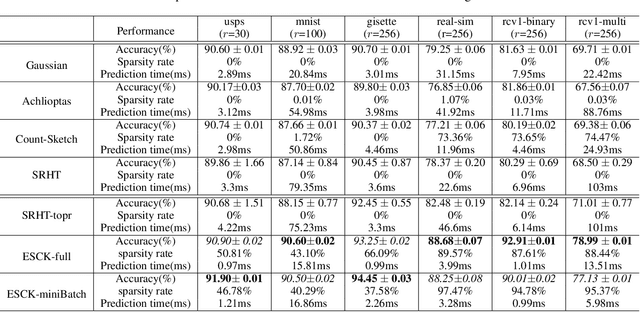
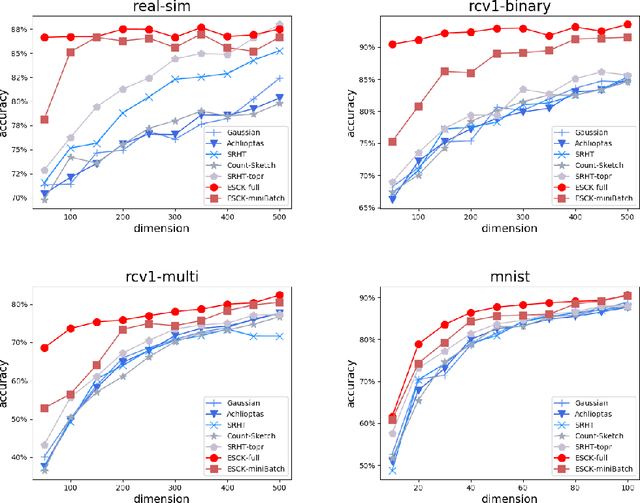
Count-sketch is a popular matrix sketching algorithm that can produce a sketch of an input data matrix X in O(nnz(X))time where nnz(X) denotes the number of non-zero entries in X. The sketched matrix will be much smaller than X while preserving most of its properties. Therefore, count-sketch is widely used for addressing high-dimensionality challenge in machine learning. However, there are two main limitations of count-sketch: (1) The sketching matrix used count-sketch is generated randomly which does not consider any intrinsic data properties of X. This data-oblivious matrix sketching method could produce a bad sketched matrix which will result in low accuracy for subsequent machine learning tasks (e.g.classification); (2) For highly sparse input data, count-sketch could produce a dense sketched data matrix. This dense sketch matrix could make the subsequent machine learning tasks more computationally expensive than on the original sparse data X. To address these two limitations, we first show an interesting connection between count-sketch and k-means clustering by analyzing the reconstruction error of the count-sketch method. Based on our analysis, we propose to reduce the reconstruction error of count-sketch by using k-means clustering algorithm to obtain the low-dimensional sketched matrix. In addition, we propose to solve k-mean clustering using gradient descent with -L1 ball projection to produce a sparse sketched matrix. Our experimental results based on six real-life classification datasets have demonstrated that our proposed method achieves higher accuracy than the original count-sketch and other popular matrix sketching algorithms. Our results also demonstrate that our method produces a sparser sketched data matrix than other methods and therefore the prediction cost of our method will be smaller than other matrix sketching methods.

Memory and Computation-Efficient Kernel SVM via Binary Embedding and Ternary Model Coefficients

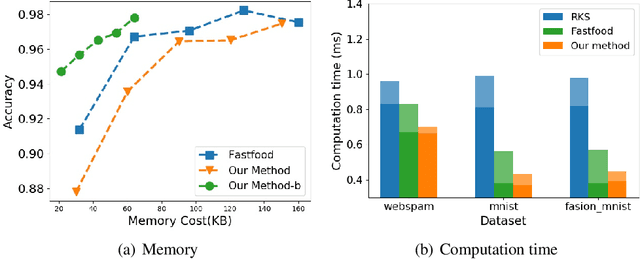
Kernel approximation is widely used to scale up kernel SVM training and prediction. However, the memory and computation costs of kernel approximation models are still too high if we want to deploy them on memory-limited devices such as mobile phones, smartwatches, and IoT devices. To address this challenge, we propose a novel memory and computation-efficient kernel SVM model by using both binary embedding and binary model coefficients. First, we propose an efficient way to generate compact binary embedding of the data, preserving the kernel similarity. Second, we propose a simple but effective algorithm to learn a linear classification model with ternary coefficients that can support different types of loss function and regularizer. Our algorithm can achieve better generalization accuracy than existing works on learning binary coefficients since we allow coefficient to be $-1$, $0$, or $1$ during the training stage, and coefficient $0$ can be removed during model inference for binary classification. Moreover, we provide a detailed analysis of the convergence of our algorithm and the inference complexity of our model. The analysis shows that the convergence to a local optimum is guaranteed, and the inference complexity of our model is much lower than other competing methods. Our experimental results on five large real-world datasets have demonstrated that our proposed method can build accurate nonlinear SVM models with memory costs less than 30KB.

Improved Subsampled Randomized Hadamard Transform for Linear SVM

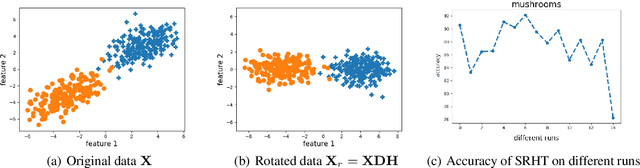
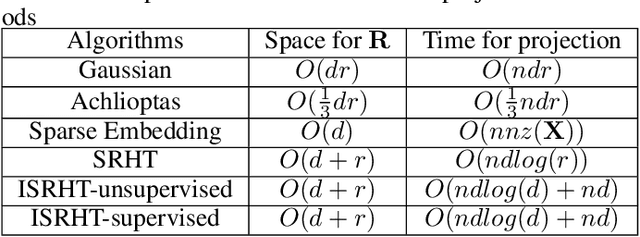
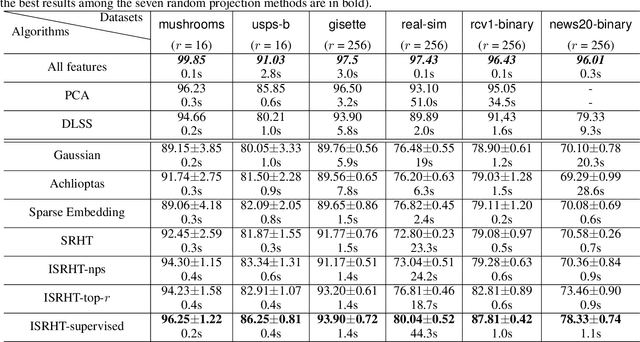
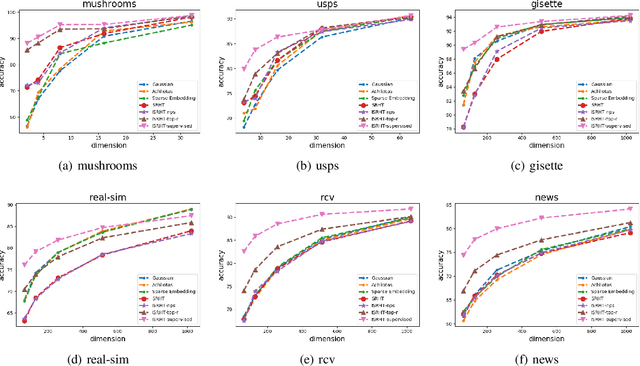
Subsampled Randomized Hadamard Transform (SRHT), a popular random projection method that can efficiently project a $d$-dimensional data into $r$-dimensional space ($r \ll d$) in $O(dlog(d))$ time, has been widely used to address the challenge of high-dimensionality in machine learning. SRHT works by rotating the input data matrix $\mathbf{X} \in \mathbb{R}^{n \times d}$ by Randomized Walsh-Hadamard Transform followed with a subsequent uniform column sampling on the rotated matrix. Despite the advantages of SRHT, one limitation of SRHT is that it generates the new low-dimensional embedding without considering any specific properties of a given dataset. Therefore, this data-independent random projection method may result in inferior and unstable performance when used for a particular machine learning task, e.g., classification. To overcome this limitation, we analyze the effect of using SRHT for random projection in the context of linear SVM classification. Based on our analysis, we propose importance sampling and deterministic top-$r$ sampling to produce effective low-dimensional embedding instead of uniform sampling SRHT. In addition, we also proposed a new supervised non-uniform sampling method. Our experimental results have demonstrated that our proposed methods can achieve higher classification accuracies than SRHT and other random projection methods on six real-life datasets.