FedPID: An Aggregation Method for Federated Learning

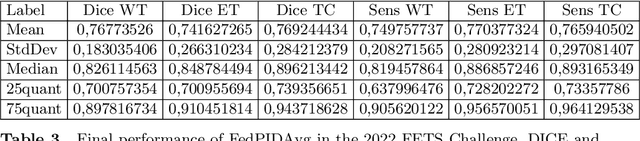
This paper presents FedPID, our submission to the Federated Tumor Segmentation Challenge 2024 (FETS24). Inspired by FedCostWAvg and FedPIDAvg, our winning contributions to FETS21 and FETS2022, we propose an improved aggregation strategy for federated and collaborative learning. FedCostWAvg is a method that averages results by considering both the number of training samples in each group and how much the cost function decreased in the last round of training. This is similar to how the derivative part of a PID controller works. In FedPIDAvg, we also included the integral part that was missing. Another challenge we faced were vastly differing dataset sizes at each center. We solved this by assuming the sizes follow a Poisson distribution and adjusting the training iterations for each center accordingly. Essentially, this part of the method controls that outliers that require too much training time are less frequently used. Based on these contributions we now adapted FedPIDAvg by changing how the integral part is computed. Instead of integrating the loss function we measure the global drop in cost since the first round.

FedPIDAvg: A PID controller inspired aggregation method for Federated Learning

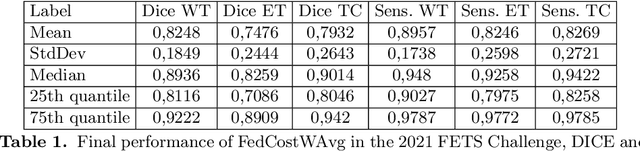
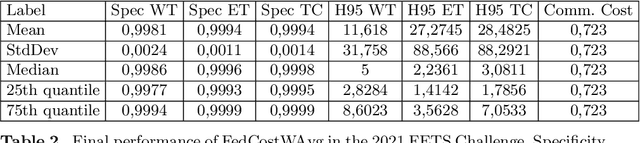
This paper presents FedPIDAvg, the winning submission to the Federated Tumor Segmentation Challenge 2022 (FETS22). Inspired by FedCostWAvg, our winning contribution to FETS21, we contribute an improved aggregation strategy for federated and collaborative learning. FedCostWAvg is a weighted averaging method that not only considers the number of training samples of each cluster but also the size of the drop of the respective cost function in the last federated round. This can be interpreted as the derivative part of a PID controller (proportional-integral-derivative controller). In FedPIDAvg, we further add the missing integral term. Another key challenge was the vastly varying size of data samples per center. We addressed this by modeling the data center sizes as following a Poisson distribution and choosing the training iterations per center accordingly. Our method outperformed all other submissions.

FedCostWAvg: A new averaging for better Federated Learning

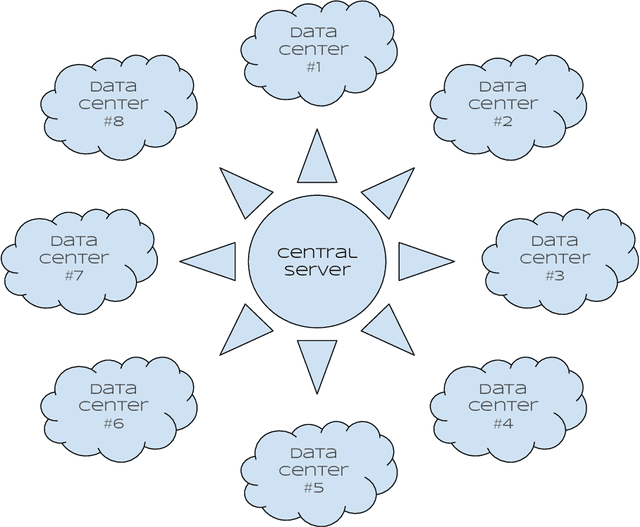
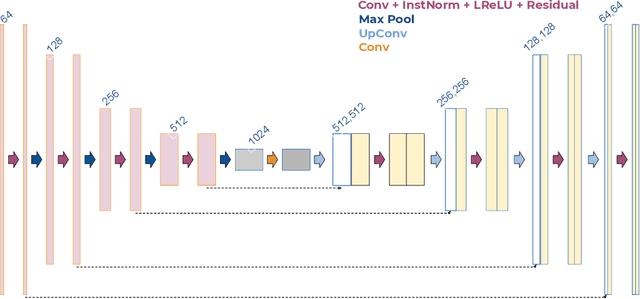
We propose a simple new aggregation strategy for federated learning that won the MICCAI Federated Tumor Segmentation Challenge 2021 (FETS), the first ever challenge on Federated Learning in the Machine Learning community. Our method addresses the problem of how to aggregate multiple models that were trained on different data sets. Conceptually, we propose a new way to choose the weights when averaging the different models, thereby extending the current state of the art (FedAvg). Empirical validation demonstrates that our approach reaches a notable improvement in segmentation performance compared to FedAvg.

Semi-Implicit Neural Solver for Time-dependent Partial Differential Equations

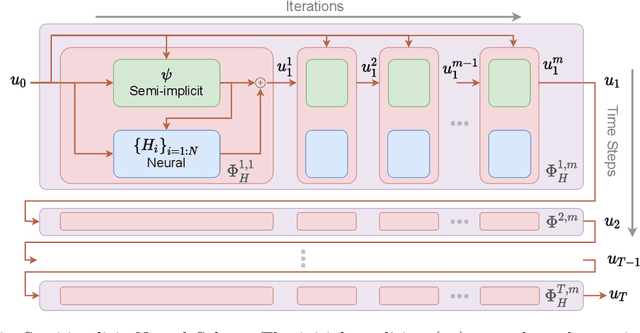
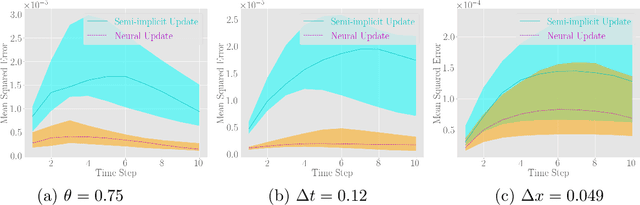
Fast and accurate solutions of time-dependent partial differential equations (PDEs) are of pivotal interest to many research fields, including physics, engineering, and biology. Generally, implicit/semi-implicit schemes are preferred over explicit ones to improve stability and correctness. However, existing semi-implicit methods are usually iterative and employ a general-purpose solver, which may be sub-optimal for a specific class of PDEs. In this paper, we propose a neural solver to learn an optimal iterative scheme in a data-driven fashion for any class of PDEs. Specifically, we modify a single iteration of a semi-implicit solver using a deep neural network. We provide theoretical guarantees for the correctness and convergence of neural solvers analogous to conventional iterative solvers. In addition to the commonly used Dirichlet boundary condition, we adopt a diffuse domain approach to incorporate a diverse type of boundary conditions, e.g., Neumann. We show that the proposed neural solver can go beyond linear PDEs and applies to a class of non-linear PDEs, where the non-linear component is non-stiff. We demonstrate the efficacy of our method on 2D and 3D scenarios. To this end, we show how our model generalizes to parameter settings, which are different from training; and achieves faster convergence than semi-implicit schemes.