Refining Counterfactual Explanations With Joint-Distribution-Informed Shapley Towards Actionable Minimality

Counterfactual explanations (CE) identify data points that closely resemble the observed data but produce different machine learning (ML) model outputs, offering critical insights into model decisions. Despite the diverse scenarios, goals and tasks to which they are tailored, existing CE methods often lack actionable efficiency because of unnecessary feature changes included within the explanations that are presented to users and stakeholders. We address this problem by proposing a method that minimizes the required feature changes while maintaining the validity of CE, without imposing restrictions on models or CE algorithms, whether instance- or group-based. The key innovation lies in computing a joint distribution between observed and counterfactual data and leveraging it to inform Shapley values for feature attributions (FA). We demonstrate that optimal transport (OT) effectively derives this distribution, especially when the alignment between observed and counterfactual data is unclear in used CE methods. Additionally, a counterintuitive finding is uncovered: it may be misleading to rely on an exact alignment defined by the CE generation mechanism in conducting FA. Our proposed method is validated on extensive experiments across multiple datasets, showcasing its effectiveness in refining CE towards greater actionable efficiency.

Self-Supervised Learning of Time Series Representation via Diffusion Process and Imputation-Interpolation-Forecasting Mask

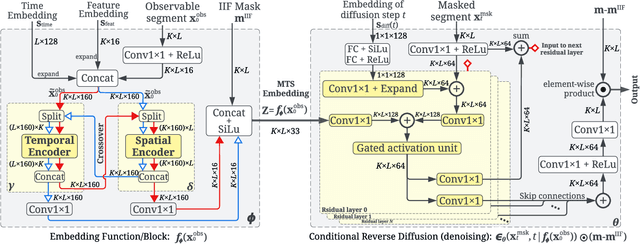
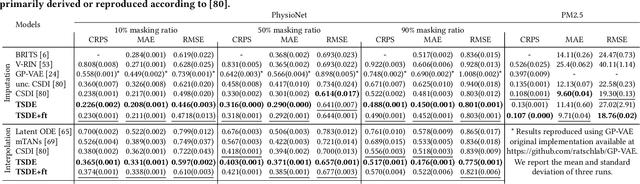
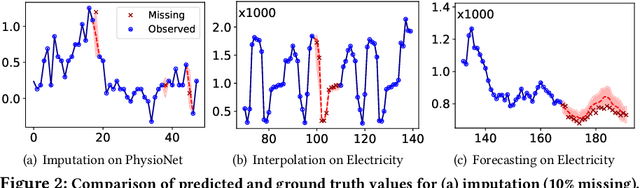
Time Series Representation Learning (TSRL) focuses on generating informative representations for various Time Series (TS) modeling tasks. Traditional Self-Supervised Learning (SSL) methods in TSRL fall into four main categories: reconstructive, adversarial, contrastive, and predictive, each with a common challenge of sensitivity to noise and intricate data nuances. Recently, diffusion-based methods have shown advanced generative capabilities. However, they primarily target specific application scenarios like imputation and forecasting, leaving a gap in leveraging diffusion models for generic TSRL. Our work, Time Series Diffusion Embedding (TSDE), bridges this gap as the first diffusion-based SSL TSRL approach. TSDE segments TS data into observed and masked parts using an Imputation-Interpolation-Forecasting (IIF) mask. It applies a trainable embedding function, featuring dual-orthogonal Transformer encoders with a crossover mechanism, to the observed part. We train a reverse diffusion process conditioned on the embeddings, designed to predict noise added to the masked part. Extensive experiments demonstrate TSDE's superiority in imputation, interpolation, forecasting, anomaly detection, classification, and clustering. We also conduct an ablation study, present embedding visualizations, and compare inference speed, further substantiating TSDE's efficiency and validity in learning representations of TS data.

DISCOUNT: Distributional Counterfactual Explanation With Optimal Transport

Counterfactual Explanations (CE) is the de facto method for providing insight and interpretability in black-box decision-making models by identifying alternative input instances that lead to different outcomes. This paper extends the concept of CEs to a distributional context, broadening the scope from individual data points to entire input and output distributions, named Distributional Counterfactual Explanation (DCE). In DCE, our focus shifts to analyzing the distributional properties of the factual and counterfactual, drawing parallels to the classical approach of assessing individual instances and their resulting decisions. We leverage Optimal Transport (OT) to frame a chance-constrained optimization problem, aiming to derive a counterfactual distribution that closely aligns with its factual counterpart, substantiated by statistical confidence. Our proposed optimization method, DISCOUNT, strategically balances this confidence across both input and output distributions. This algorithm is accompanied by an analysis of its convergence rate. The efficacy of our proposed method is substantiated through a series of illustrative case studies, highlighting its potential in providing deep insights into decision-making models.

Robust Network Pruning With Sparse Entropic Wasserstein Regression

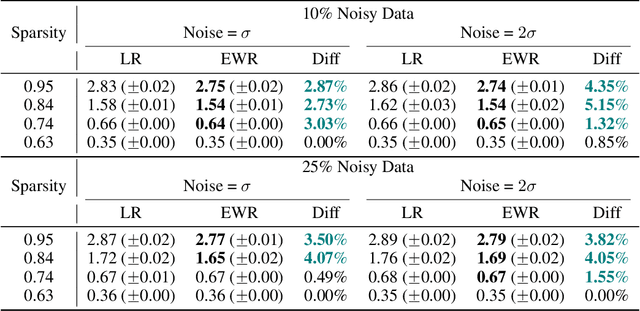
This study unveils a cutting-edge technique for neural network pruning that judiciously addresses noisy gradients during the computation of the empirical Fisher Information Matrix (FIM). We introduce an entropic Wasserstein regression (EWR) formulation, capitalizing on the geometric attributes of the optimal transport (OT) problem. This is analytically showcased to excel in noise mitigation by adopting neighborhood interpolation across data points. The unique strength of the Wasserstein distance is its intrinsic ability to strike a balance between noise reduction and covariance information preservation. Extensive experiments performed on various networks show comparable performance of the proposed method with state-of-the-art (SoTA) network pruning algorithms. Our proposed method outperforms the SoTA when the network size or the target sparsity is large, the gain is even larger with the existence of noisy gradients, possibly from noisy data, analog memory, or adversarial attacks. Notably, our proposed method achieves a gain of 6% improvement in accuracy and 8% improvement in testing loss for MobileNetV1 with less than one-fourth of the network parameters remaining.

Weighted Sum-Rate Maximization With Causal Inference for Latent Interference Estimation

The paper investigates the weighted sum-rate maximization (WSRM) problem with latent interfering sources outside the known network, whose power allocation policy is hidden from and uncontrollable to optimization. The paper extends the famous alternate optimization algorithm weighted minimum mean square error (WMMSE) [1] under a causal inference framework to tackle with WSRM under latent interference. Namely, with the possibility of power policy shifting in the hidden network, computing an iterating direction based on the observed interference inherently implies that counterfactual is ignored in decision making. A synthetic control (SC) method is used to estimate the counterfactual. For any link in the known network, SC constructs a convex combination of the interference on other links and uses it as an estimate. Power iteration is performed on the estimated rather than the observed interference. The proposed SC-WMMSE requires no more information than its origin. To our best knowledge, this is the first paper explores the potential of causal inference to assist mathematical optimization in addressing classic wireless optimization problems. Numerical results suggest the superiority of the SC-WMMSE over the original in both convergence and objective.