Robust Network Pruning With Sparse Entropic Wasserstein Regression
Paper and Code
Oct 07, 2023

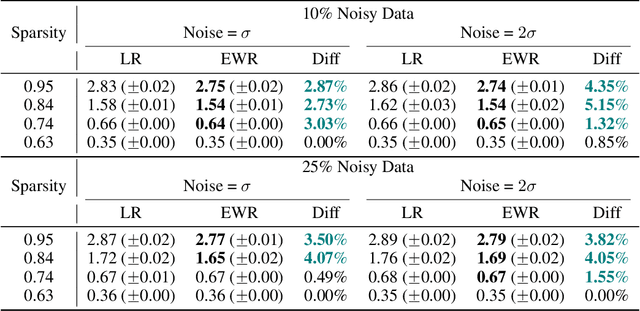

This study unveils a cutting-edge technique for neural network pruning that judiciously addresses noisy gradients during the computation of the empirical Fisher Information Matrix (FIM). We introduce an entropic Wasserstein regression (EWR) formulation, capitalizing on the geometric attributes of the optimal transport (OT) problem. This is analytically showcased to excel in noise mitigation by adopting neighborhood interpolation across data points. The unique strength of the Wasserstein distance is its intrinsic ability to strike a balance between noise reduction and covariance information preservation. Extensive experiments performed on various networks show comparable performance of the proposed method with state-of-the-art (SoTA) network pruning algorithms. Our proposed method outperforms the SoTA when the network size or the target sparsity is large, the gain is even larger with the existence of noisy gradients, possibly from noisy data, analog memory, or adversarial attacks. Notably, our proposed method achieves a gain of 6% improvement in accuracy and 8% improvement in testing loss for MobileNetV1 with less than one-fourth of the network parameters remaining.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge