Measurable Majorities Are Not Finitely Axiomatizable

This theoretical note studies the finite axiomatizability of strict majority reasoning in finite social decision frames. Moss and Pedersen (2026) <doi: 10.48550/arXiv.2606.23853> introduce a coherence criterion that characterizes exactly when qualitative majority judgments are representable by a finitely additive measure. The question addressed here is whether that coherence criterion can be replaced, in the finite setting, by any bounded finite fragment. We prove that it cannot. For every $k\ge 1$, we construct a maximal standard frame whose shortest coherence violation has length exactly $2k+2$. Hence there is no uniform finite bound on the incoherence index of social decision frames, resolving Conjecture 5.7 stated by Moss and Pedersen (2026). The construction is geometric, in the sense that it proceeds via orthogonality and dimension in rational vector spaces, and self-contained: it isolates a symmetric family of half-sized voting blocs and extends it to a maximal frame in which every shorter balanced obstruction is excluded. Along the explicit infinite sequence of universe sizes obtained in the construction, this also establishes the middle-layer family predicted by Conjecture B.25 by Moss and Pedersen (2026). Together with the soundness and completeness theorem for the Moss-Pedersen minimal logic for strict majorities, this establishes that measurable social decision frames are not finitely axiomatizable in that language.

The Measurable Majority

This paper studies strict majority reasoning in finite electorates using so-called $\textit{social decision frames}$: finite sets of voters equipped with distinguished families of coalitions interpreted as those voting blocs evaluated to form a strict majority. A coherence criterion for qualitative majority judgments is identified and shown to give an exact characterization for representability of strict majorities by finitely additive measures. In addition, a minimal natural logic for reasoning about strict majorities is shown to be sound and complete. These developments motivate examination of associated combinatorial questions concerning incoherence in finite families of sets; partial results and a conjecture are given. Finally, the results of this paper are applied to correct a classical representation theorem for weak qualitative probability structures due to Patrick Suppes and to establish a May-type characterization for ordinary strict majority rule for social decision frames.

Extracting Mathematical Concepts with Large Language Models

We extract mathematical concepts from mathematical text using generative large language models (LLMs) like ChatGPT, contributing to the field of automatic term extraction (ATE) and mathematical text processing, and also to the study of LLMs themselves. Our work builds on that of others in that we aim for automatic extraction of terms (keywords) in one mathematical field, category theory, using as a corpus the 755 abstracts from a snapshot of the online journal "Theory and Applications of Categories", circa 2020. Where our study diverges from previous work is in (1) providing a more thorough analysis of what makes mathematical term extraction a difficult problem to begin with; (2) paying close attention to inter-annotator disagreements; (3) providing a set of guidelines which both human and machine annotators could use to standardize the extraction process; (4) introducing a new annotation tool to help humans with ATE, applicable to any mathematical field and even beyond mathematics; (5) using prompts to ChatGPT as part of the extraction process, and proposing best practices for such prompts; and (6) raising the question of whether ChatGPT could be used as an annotator on the same level as human experts. Our overall findings are that the matter of mathematical ATE is an interesting field which can benefit from participation by LLMs, but LLMs themselves cannot at this time surpass human performance on it.

NeuralLog: Natural Language Inference with Joint Neural and Logical Reasoning

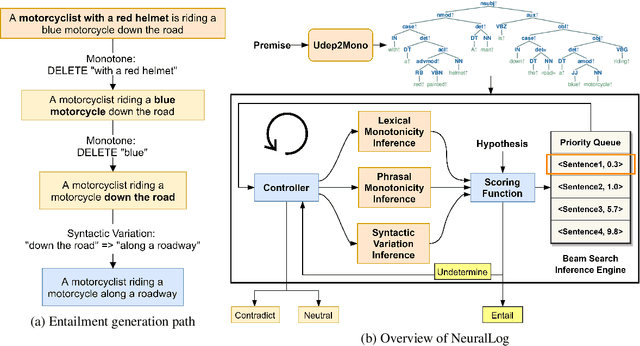
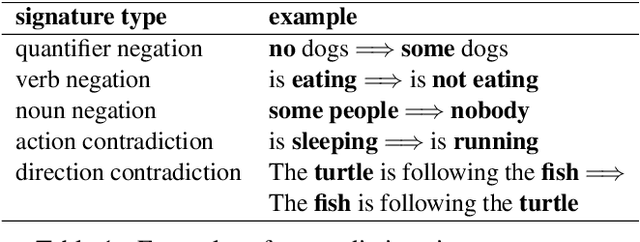
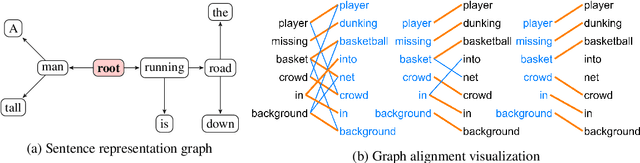
Deep learning (DL) based language models achieve high performance on various benchmarks for Natural Language Inference (NLI). And at this time, symbolic approaches to NLI are receiving less attention. Both approaches (symbolic and DL) have their advantages and weaknesses. However, currently, no method combines them in a system to solve the task of NLI. To merge symbolic and deep learning methods, we propose an inference framework called NeuralLog, which utilizes both a monotonicity-based logical inference engine and a neural network language model for phrase alignment. Our framework models the NLI task as a classic search problem and uses the beam search algorithm to search for optimal inference paths. Experiments show that our joint logic and neural inference system improves accuracy on the NLI task and can achieve state-of-art accuracy on the SICK and MED datasets.

OCNLI: Original Chinese Natural Language Inference

Despite the tremendous recent progress on natural language inference (NLI), driven largely by large-scale investment in new datasets (e.g., SNLI, MNLI) and advances in modeling, most progress has been limited to English due to a lack of reliable datasets for most of the world's languages. In this paper, we present the first large-scale NLI dataset (consisting of ~56,000 annotated sentence pairs) for Chinese called the Original Chinese Natural Language Inference dataset (OCNLI). Unlike recent attempts at extending NLI to other languages, our dataset does not rely on any automatic translation or non-expert annotation. Instead, we elicit annotations from native speakers specializing in linguistics. We follow closely the annotation protocol used for MNLI, but create new strategies for eliciting diverse hypotheses. We establish several baseline results on our dataset using state-of-the-art pre-trained models for Chinese, and find even the best performing models to be far outpaced by human performance (~12% absolute performance gap), making it a challenging new resource that we hope will help to accelerate progress in Chinese NLU. To the best of our knowledge, this is the first human-elicited MNLI-style corpus for a non-English language.

MonaLog: a Lightweight System for Natural Language Inference Based on Monotonicity

We present a new logic-based inference engine for natural language inference (NLI) called MonaLog, which is based on natural logic and the monotonicity calculus. In contrast to existing logic-based approaches, our system is intentionally designed to be as lightweight as possible, and operates using a small set of well-known (surface-level) monotonicity facts about quantifiers, lexical items and tokenlevel polarity information. Despite its simplicity, we find our approach to be competitive with other logic-based NLI models on the SICK benchmark. We also use MonaLog in combination with the current state-of-the-art model BERT in a variety of settings, including for compositional data augmentation. We show that MonaLog is capable of generating large amounts of high-quality training data for BERT, improving its accuracy on SICK.

Probing Natural Language Inference Models through Semantic Fragments

Do state-of-the-art models for language understanding already have, or can they easily learn, abilities such as boolean coordination, quantification, conditionals, comparatives, and monotonicity reasoning (i.e., reasoning about word substitutions in sentential contexts)? While such phenomena are involved in natural language inference (NLI) and go beyond basic linguistic understanding, it is unclear the extent to which they are captured in existing NLI benchmarks and effectively learned by models. To investigate this, we propose the use of semantic fragments---systematically generated datasets that each target a different semantic phenomenon---for probing, and efficiently improving, such capabilities of linguistic models. This approach to creating challenge datasets allows direct control over the semantic diversity and complexity of the targeted linguistic phenomena, and results in a more precise characterization of a model's linguistic behavior. Our experiments, using a library of 8 such semantic fragments, reveal two remarkable findings: (a) State-of-the-art models, including BERT, that are pre-trained on existing NLI benchmark datasets perform poorly on these new fragments, even though the phenomena probed here are central to the NLI task. (b) On the other hand, with only a few minutes of additional fine-tuning---with a carefully selected learning rate and a novel variation of "inoculation"---a BERT-based model can master all of these logic and monotonicity fragments while retaining its performance on established NLI benchmarks.

Exploring the Landscape of Relational Syllogistic Logics

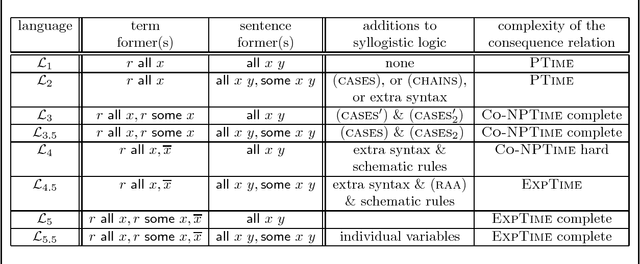
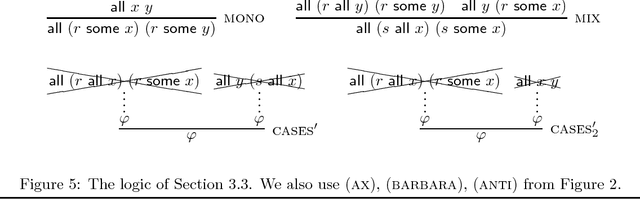
This paper explores relational syllogistic logics, a family of logical systems related to reasoning about relations in extensions of the classical syllogistic. These are all decidable logical systems. We prove completeness theorems and complexity results for a natural subfamily of relational syllogistic logics, parametrized by constructors for terms and for sentences.

Logics for the Relational Syllogistic

The Aristotelian syllogistic cannot account for the validity of many inferences involving relational facts. In this paper, we investigate the prospects for providing a relational syllogistic. We identify several fragments based on (a) whether negation is permitted on all nouns, including those in the subject of a sentence; and (b) whether the subject noun phrase may contain a relative clause. The logics we present are extensions of the classical syllogistic, and we pay special attention to the question of whether reductio ad absurdum is needed. Thus our main goal is to derive results on the existence (or non-existence) of syllogistic proof systems for relational fragments. We also determine the computational complexity of all our fragments.