Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Alex Kruckman
Exploring the Landscape of Relational Syllogistic Logics
Sep 03, 2018Figures and Tables: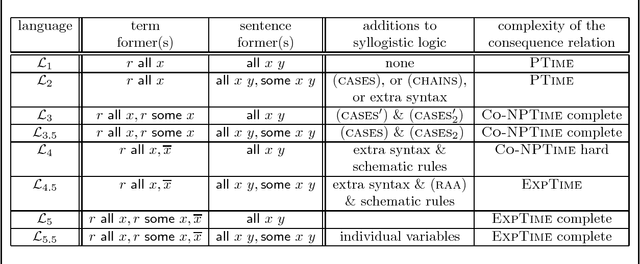


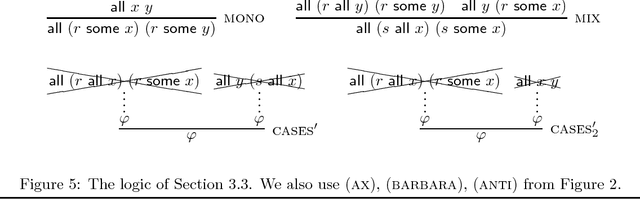




Abstract:This paper explores relational syllogistic logics, a family of logical systems related to reasoning about relations in extensions of the classical syllogistic. These are all decidable logical systems. We prove completeness theorems and complexity results for a natural subfamily of relational syllogistic logics, parametrized by constructors for terms and for sentences.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge