Shaping Up SHAP: Enhancing Stability through Layer-Wise Neighbor Selection

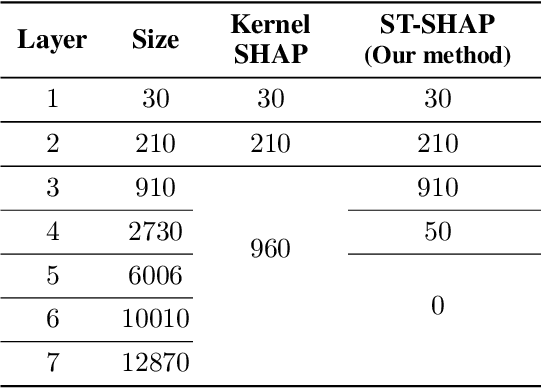
Machine learning techniques, such as deep learning and ensemble methods, are widely used in various domains due to their ability to handle complex real-world tasks. However, their black-box nature has raised multiple concerns about the fairness, trustworthiness, and transparency of computer-assisted decision-making. This has led to the emergence of local post-hoc explainability methods, which offer explanations for individual decisions made by black-box algorithms. Among these methods, Kernel SHAP is widely used due to its model-agnostic nature and its well-founded theoretical framework. Despite these strengths, Kernel SHAP suffers from high instability: different executions of the method with the same inputs can lead to significantly different explanations, which diminishes the utility of post-hoc explainability. The contribution of this paper is two-fold. On the one hand, we show that Kernel SHAP's instability is caused by its stochastic neighbor selection procedure, which we adapt to achieve full stability without compromising explanation fidelity. On the other hand, we show that by restricting the neighbors generation to perturbations of size 1 -- which we call the coalitions of Layer 1 -- we obtain a novel feature-attribution method that is fully stable, efficient to compute, and still meaningful.

Persistence-Based Discretization for Learning Discrete Event Systems from Time Series

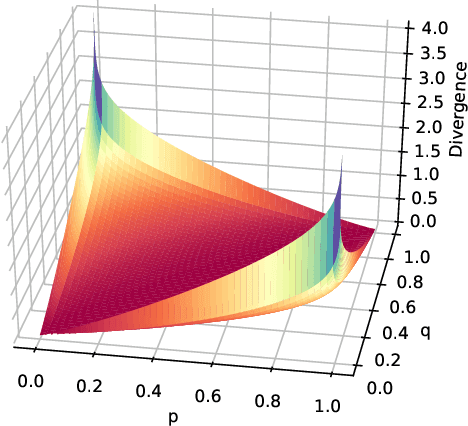
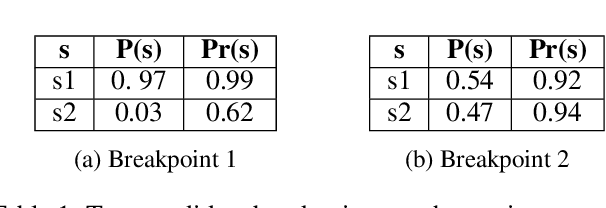
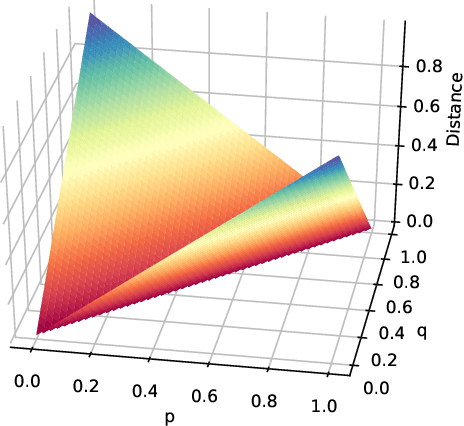
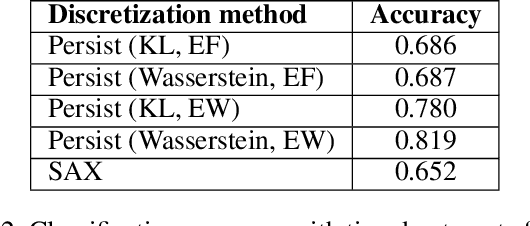
To get a good understanding of a dynamical system, it is convenient to have an interpretable and versatile model of it. Timed discrete event systems are a kind of model that respond to these requirements. However, such models can be inferred from timestamped event sequences but not directly from numerical data. To solve this problem, a discretization step must be done to identify events or symbols in the time series. Persist is a discretization method that intends to create persisting symbols by using a score called persistence score. This allows to mitigate the risk of undesirable symbol changes that would lead to a too complex model. After the study of the persistence score, we point out that it tends to favor excessive cases making it miss interesting persisting symbols. To correct this behavior, we replace the metric used in the persistence score, the Kullback-Leibler divergence, with the Wasserstein distance. Experiments show that the improved persistence score enhances Persist's ability to capture the information of the original time series and that it makes it better suited for discrete event systems learning.

s-LIME: Reconciling Locality and Fidelity in Linear Explanations

The benefit of locality is one of the major premises of LIME, one of the most prominent methods to explain black-box machine learning models. This emphasis relies on the postulate that the more locally we look at the vicinity of an instance, the simpler the black-box model becomes, and the more accurately we can mimic it with a linear surrogate. As logical as this seems, our findings suggest that, with the current design of LIME, the surrogate model may degenerate when the explanation is too local, namely, when the bandwidth parameter $\sigma$ tends to zero. Based on this observation, the contribution of this paper is twofold. Firstly, we study the impact of both the bandwidth and the training vicinity on the fidelity and semantics of LIME explanations. Secondly, and based on our findings, we propose \slime, an extension of LIME that reconciles fidelity and locality.

Day-ahead time series forecasting: application to capacity planning

In the context of capacity planning, forecasting the evolution of informatics servers usage enables companies to better manage their computational resources. We address this problem by collecting key indicator time series and propose to forecast their evolution a day-ahead. Our method assumes that data is structured by a daily seasonality, but also that there is typical evolution of indicators within a day. Then, it uses the combination of a clustering algorithm and Markov Models to produce day-ahead forecasts. Our experiments on real datasets show that the data satisfies our assumption and that, in the case study, our method outperforms classical approaches (AR, Holt-Winters).