SpaceTime: Causal Discovery from Non-Stationary Time Series

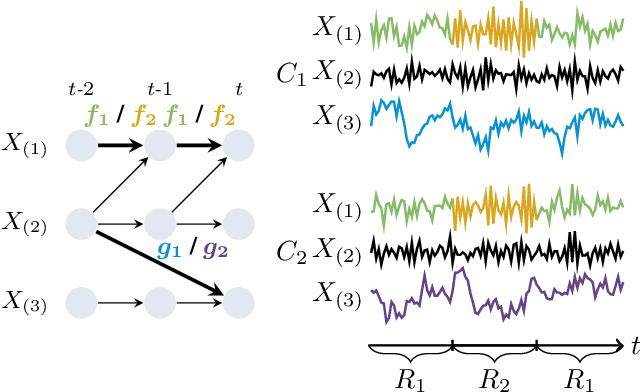
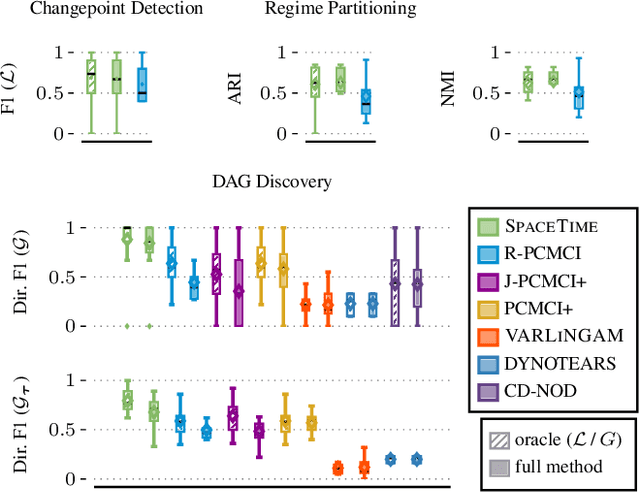
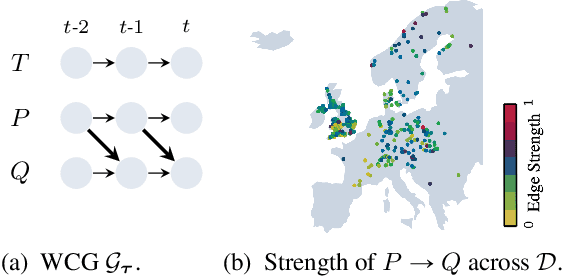
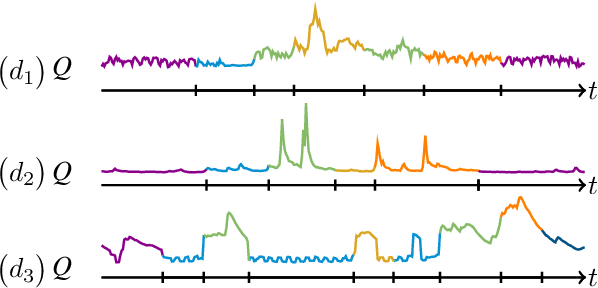
Understanding causality is challenging and often complicated by changing causal relationships over time and across environments. Climate patterns, for example, shift over time with recurring seasonal trends, while also depending on geographical characteristics such as ecosystem variability. Existing methods for discovering causal graphs from time series either assume stationarity, do not permit both temporal and spatial distribution changes, or are unaware of locations with the same causal relationships. In this work, we therefore unify the three tasks of causal graph discovery in the non-stationary multi-context setting, of reconstructing temporal regimes, and of partitioning datasets and time intervals into those where invariant causal relationships hold. To construct a consistent score that forms the basis of our method, we employ the Minimum Description Length principle. Our resulting algorithm SPACETIME simultaneously accounts for heterogeneity across space and non-stationarity over time. Given multiple time series, it discovers regime changepoints and a temporal causal graph using non-parametric functional modeling and kernelized discrepancy testing. We also show that our method provides insights into real-world phenomena such as river-runoff measured at different catchments and biosphere-atmosphere interactions across ecosystems.

Persistence-Based Discretization for Learning Discrete Event Systems from Time Series

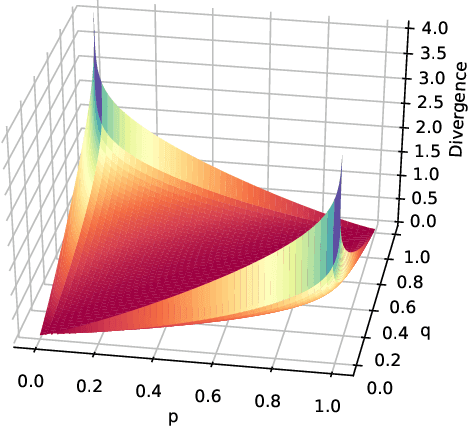
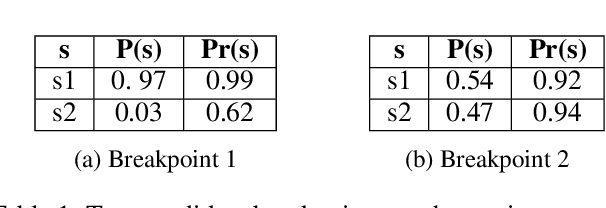
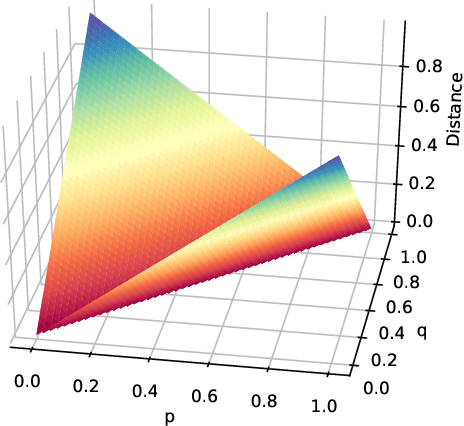
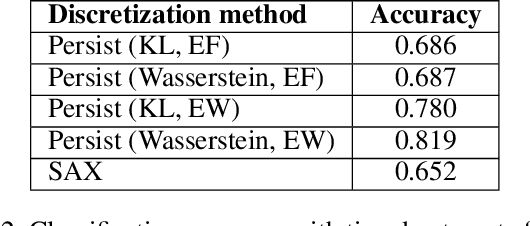
To get a good understanding of a dynamical system, it is convenient to have an interpretable and versatile model of it. Timed discrete event systems are a kind of model that respond to these requirements. However, such models can be inferred from timestamped event sequences but not directly from numerical data. To solve this problem, a discretization step must be done to identify events or symbols in the time series. Persist is a discretization method that intends to create persisting symbols by using a score called persistence score. This allows to mitigate the risk of undesirable symbol changes that would lead to a too complex model. After the study of the persistence score, we point out that it tends to favor excessive cases making it miss interesting persisting symbols. To correct this behavior, we replace the metric used in the persistence score, the Kullback-Leibler divergence, with the Wasserstein distance. Experiments show that the improved persistence score enhances Persist's ability to capture the information of the original time series and that it makes it better suited for discrete event systems learning.