Does It Make Sense to Explain a Black Box With Another Black Box?

Although counterfactual explanations are a popular approach to explain ML black-box classifiers, they are less widespread in NLP. Most methods find those explanations by iteratively perturbing the target document until it is classified differently by the black box. We identify two main families of counterfactual explanation methods in the literature, namely, (a) \emph{transparent} methods that perturb the target by adding, removing, or replacing words, and (b) \emph{opaque} approaches that project the target document into a latent, non-interpretable space where the perturbation is carried out subsequently. This article offers a comparative study of the performance of these two families of methods on three classical NLP tasks. Our empirical evidence shows that opaque approaches can be an overkill for downstream applications such as fake news detection or sentiment analysis since they add an additional level of complexity with no significant performance gain. These observations motivate our discussion, which raises the question of whether it makes sense to explain a black box using another black box.

Persistence-Based Discretization for Learning Discrete Event Systems from Time Series

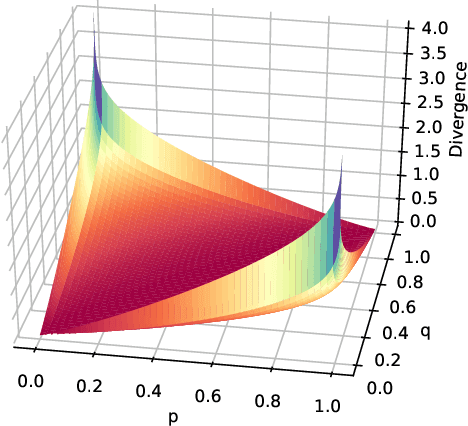
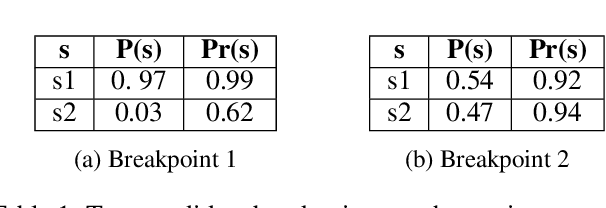
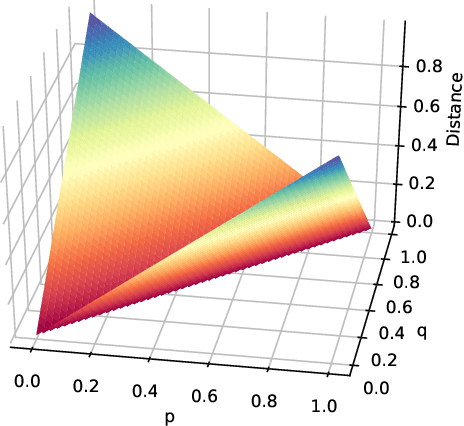
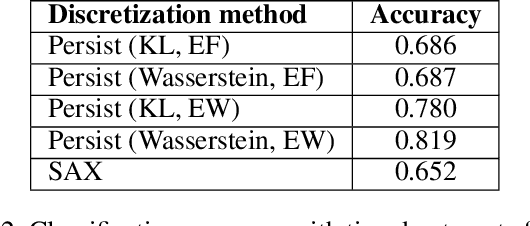
To get a good understanding of a dynamical system, it is convenient to have an interpretable and versatile model of it. Timed discrete event systems are a kind of model that respond to these requirements. However, such models can be inferred from timestamped event sequences but not directly from numerical data. To solve this problem, a discretization step must be done to identify events or symbols in the time series. Persist is a discretization method that intends to create persisting symbols by using a score called persistence score. This allows to mitigate the risk of undesirable symbol changes that would lead to a too complex model. After the study of the persistence score, we point out that it tends to favor excessive cases making it miss interesting persisting symbols. To correct this behavior, we replace the metric used in the persistence score, the Kullback-Leibler divergence, with the Wasserstein distance. Experiments show that the improved persistence score enhances Persist's ability to capture the information of the original time series and that it makes it better suited for discrete event systems learning.