KiJung Yoon
Reviving and Improving Recurrent Back-Propagation
Aug 13, 2018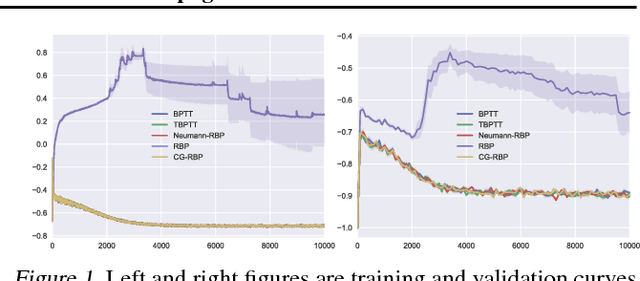
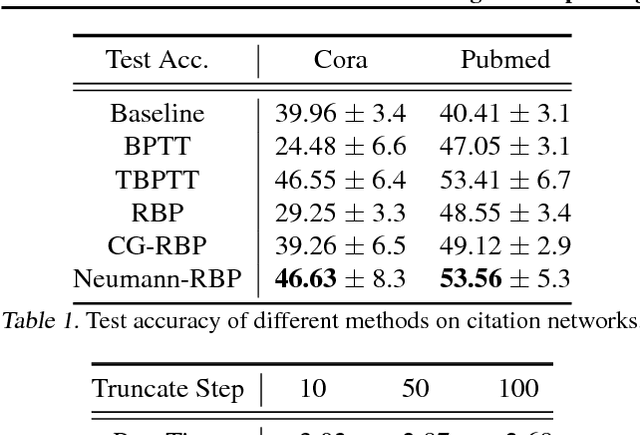

Abstract:In this paper, we revisit the recurrent back-propagation (RBP) algorithm, discuss the conditions under which it applies as well as how to satisfy them in deep neural networks. We show that RBP can be unstable and propose two variants based on conjugate gradient on the normal equations (CG-RBP) and Neumann series (Neumann-RBP). We further investigate the relationship between Neumann-RBP and back propagation through time (BPTT) and its truncated version (TBPTT). Our Neumann-RBP has the same time complexity as TBPTT but only requires constant memory, whereas TBPTT's memory cost scales linearly with the number of truncation steps. We examine all RBP variants along with BPTT and TBPTT in three different application domains: associative memory with continuous Hopfield networks, document classification in citation networks using graph neural networks and hyperparameter optimization for fully connected networks. All experiments demonstrate that RBPs, especially the Neumann-RBP variant, are efficient and effective for optimizing convergent recurrent neural networks.
Inference in Probabilistic Graphical Models by Graph Neural Networks
May 25, 2018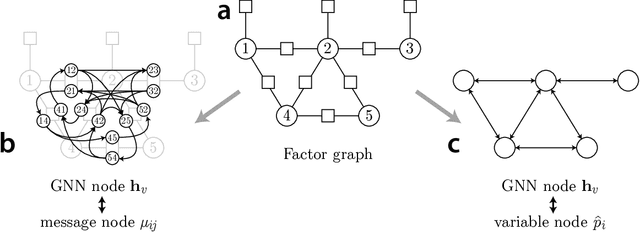
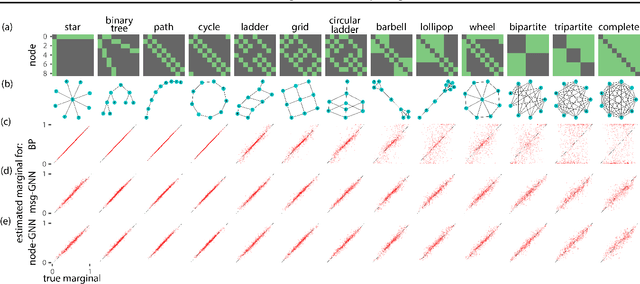
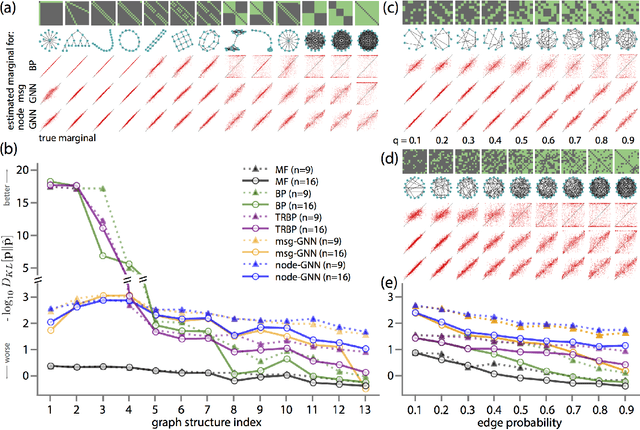
Abstract:A fundamental computation for statistical inference and accurate decision-making is to compute the marginal probabilities or most probable states of task-relevant variables. Probabilistic graphical models can efficiently represent the structure of such complex data, but performing these inferences is generally difficult. Message-passing algorithms, such as belief propagation, are a natural way to disseminate evidence amongst correlated variables while exploiting the graph structure, but these algorithms can struggle when the conditional dependency graphs contain loops. Here we use Graph Neural Networks (GNNs) to learn a message-passing algorithm that solves these inference tasks. We first show that the architecture of GNNs is well-matched to inference tasks. We then demonstrate the efficacy of this inference approach by training GNNs on a collection of graphical models and showing that they substantially outperform belief propagation on loopy graphs. Our message-passing algorithms generalize out of the training set to larger graphs and graphs with different structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge