Reviving and Improving Recurrent Back-Propagation
Paper and Code
Aug 13, 2018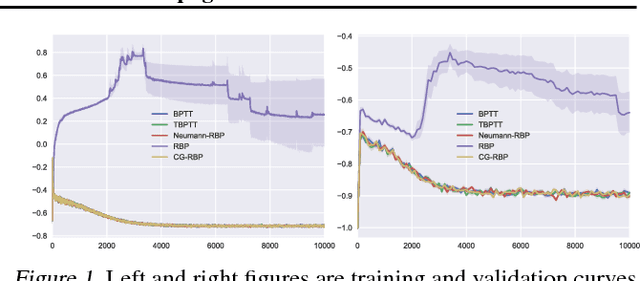
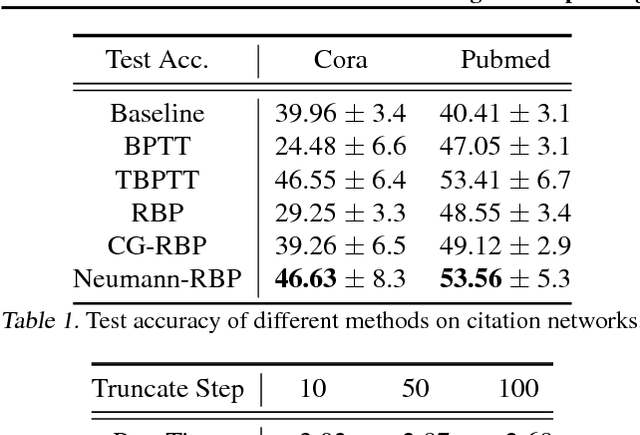
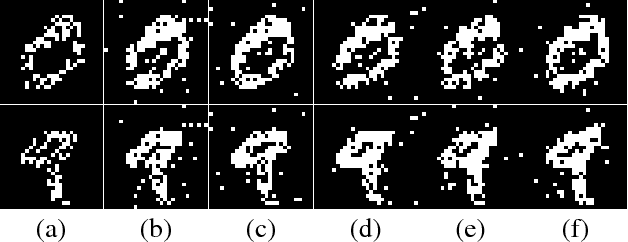

In this paper, we revisit the recurrent back-propagation (RBP) algorithm, discuss the conditions under which it applies as well as how to satisfy them in deep neural networks. We show that RBP can be unstable and propose two variants based on conjugate gradient on the normal equations (CG-RBP) and Neumann series (Neumann-RBP). We further investigate the relationship between Neumann-RBP and back propagation through time (BPTT) and its truncated version (TBPTT). Our Neumann-RBP has the same time complexity as TBPTT but only requires constant memory, whereas TBPTT's memory cost scales linearly with the number of truncation steps. We examine all RBP variants along with BPTT and TBPTT in three different application domains: associative memory with continuous Hopfield networks, document classification in citation networks using graph neural networks and hyperparameter optimization for fully connected networks. All experiments demonstrate that RBPs, especially the Neumann-RBP variant, are efficient and effective for optimizing convergent recurrent neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge