Theoretical Analysis of Leave-one-out Cross Validation for Non-differentiable Penalties under High-dimensional Settings

Despite a large and significant body of recent work focused on estimating the out-of-sample risk of regularized models in the high dimensional regime, a theoretical understanding of this problem for non-differentiable penalties such as generalized LASSO and nuclear norm is missing. In this paper we resolve this challenge. We study this problem in the proportional high dimensional regime where both the sample size n and number of features p are large, and n/p and the signal-to-noise ratio (per observation) remain finite. We provide finite sample upper bounds on the expected squared error of leave-one-out cross-validation (LO) in estimating the out-of-sample risk. The theoretical framework presented here provides a solid foundation for elucidating empirical findings that show the accuracy of LO.

Approximate Leave-one-out Cross Validation for Regression with $\ell_1$ Regularizers (extended version)

The out-of-sample error (OO) is the main quantity of interest in risk estimation and model selection. Leave-one-out cross validation (LO) offers a (nearly) distribution-free yet computationally demanding approach to estimate OO. Recent theoretical work showed that approximate leave-one-out cross validation (ALO) is a computationally efficient and statistically reliable estimate of LO (and OO) for generalized linear models with differentiable regularizers. For problems involving non-differentiable regularizers, despite significant empirical evidence, the theoretical understanding of ALO's error remains unknown. In this paper, we present a novel theory for a wide class of problems in the generalized linear model family with non-differentiable regularizers. We bound the error |ALO - LO| in terms of intuitive metrics such as the size of leave-i-out perturbations in active sets, sample size n, number of features p and regularization parameters. As a consequence, for the $\ell_1$-regularized problems, we show that |ALO - LO| goes to zero as p goes to infinity while n/p and SNR are fixed and bounded.

Error bounds in estimating the out-of-sample prediction error using leave-one-out cross validation in high-dimensions

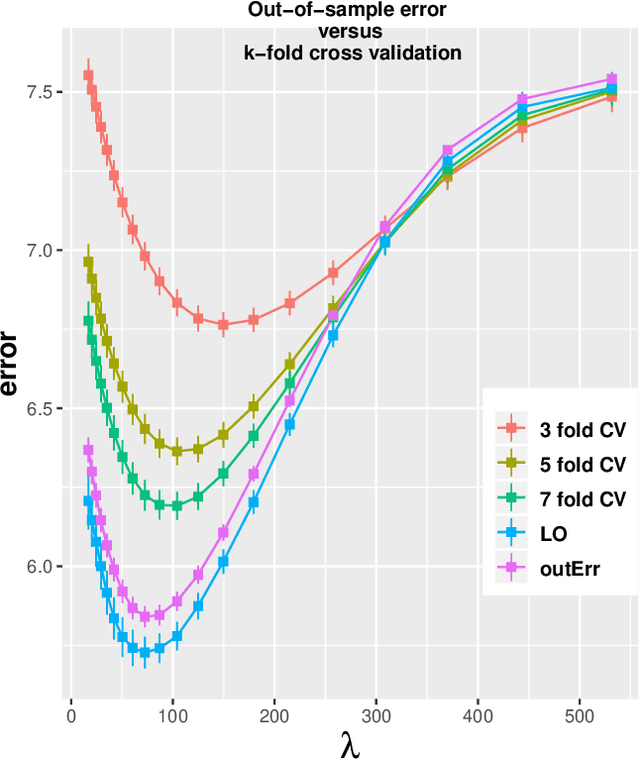
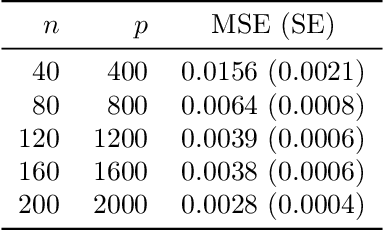
We study the problem of out-of-sample risk estimation in the high dimensional regime where both the sample size $n$ and number of features $p$ are large, and $n/p$ can be less than one. Extensive empirical evidence confirms the accuracy of leave-one-out cross validation (LO) for out-of-sample risk estimation. Yet, a unifying theoretical evaluation of the accuracy of LO in high-dimensional problems has remained an open problem. This paper aims to fill this gap for penalized regression in the generalized linear family. With minor assumptions about the data generating process, and without any sparsity assumptions on the regression coefficients, our theoretical analysis obtains finite sample upper bounds on the expected squared error of LO in estimating the out-of-sample error. Our bounds show that the error goes to zero as $n,p \rightarrow \infty$, even when the dimension $p$ of the feature vectors is comparable with or greater than the sample size $n$. One technical advantage of the theory is that it can be used to clarify and connect some results from the recent literature on scalable approximate LO.

Consistent Risk Estimation in High-Dimensional Linear Regression

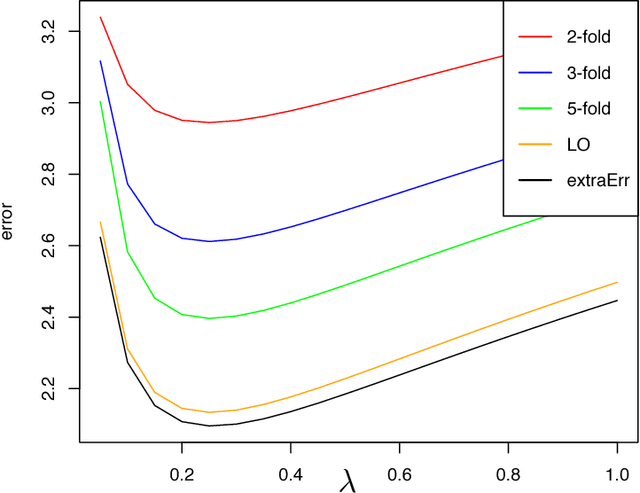
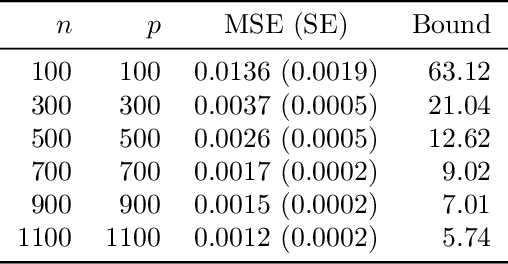
Risk estimation is at the core of many learning systems. The importance of this problem has motivated researchers to propose different schemes, such as cross validation, generalized cross validation, and Bootstrap. The theoretical properties of such estimates have been extensively studied in the low-dimensional settings, where the number of predictors $p$ is much smaller than the number of observations $n$. However, a unifying methodology accompanied with a rigorous theory is lacking in high-dimensional settings. This paper studies the problem of risk estimation under the high-dimensional asymptotic setting $n,p \rightarrow \infty$ and $n/p \rightarrow \delta$ ($\delta$ is a fixed number), and proves the consistency of three risk estimates that have been successful in numerical studies, i.e., leave-one-out cross validation (LOOCV), approximate leave-one-out (ALO), and approximate message passing (AMP)-based techniques. A corner stone of our analysis is a bound that we obtain on the discrepancy of the `residuals' obtained from AMP and LOOCV. This connection not only enables us to obtain a more refined information on the estimates of AMP, ALO, and LOOCV, but also offers an upper bound on the convergence rate of each estimate.

Robust and scalable Bayesian analysis of spatial neural tuning function data

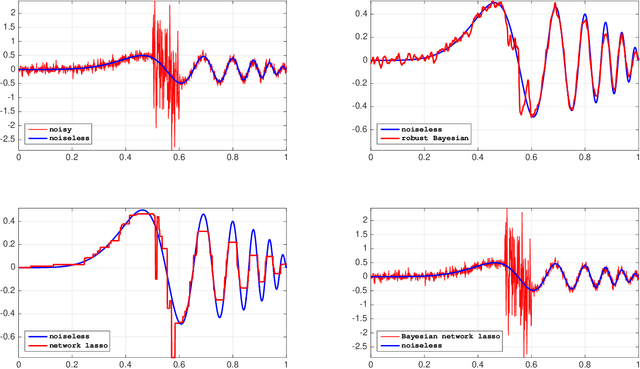
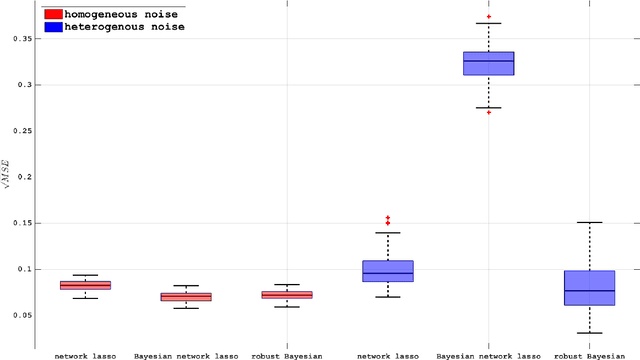
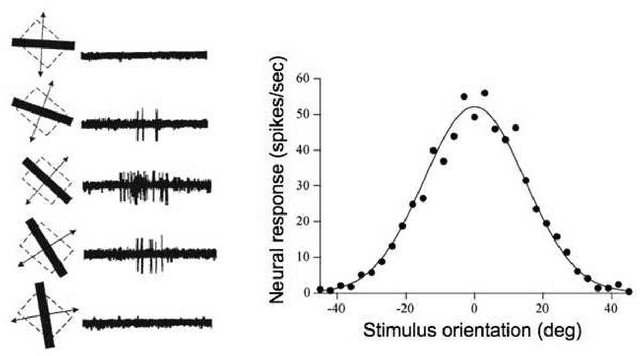
A common analytical problem in neuroscience is the interpretation of neural activity with respect to sensory input or behavioral output. This is typically achieved by regressing measured neural activity against known stimuli or behavioral variables to produce a "tuning function" for each neuron. Unfortunately, because this approach handles neurons individually, it cannot take advantage of simultaneous measurements from spatially adjacent neurons that often have similar tuning properties. On the other hand, sharing information between adjacent neurons can errantly degrade estimates of tuning functions across space if there are sharp discontinuities in tuning between nearby neurons. In this paper, we develop a computationally efficient block Gibbs sampler that effectively pools information between neurons to de-noise tuning function estimates while simultaneously preserving sharp discontinuities that might exist in the organization of tuning across space. This method is fully Bayesian and its computational cost per iteration scales sub-quadratically with total parameter dimensionality. We demonstrate the robustness and scalability of this approach by applying it to both real and synthetic datasets. In particular, an application to data from the spinal cord illustrates that the proposed methods can dramatically decrease the experimental time required to accurately estimate tuning functions.