Timothy A. Machado
Robust and scalable Bayesian analysis of spatial neural tuning function data
Jun 24, 2016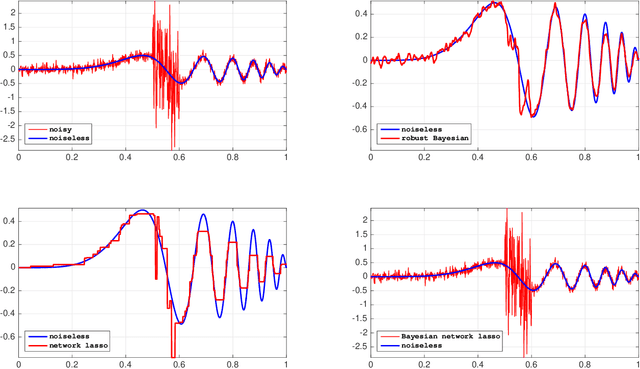
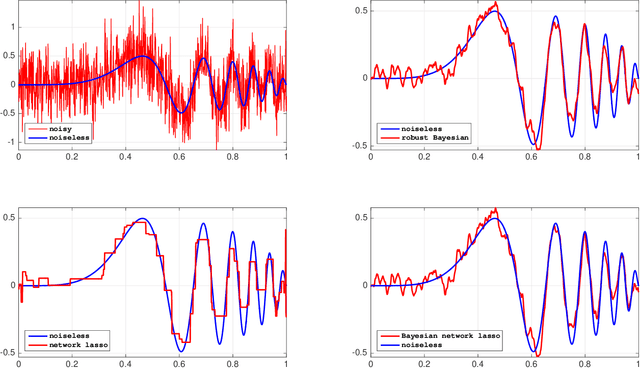
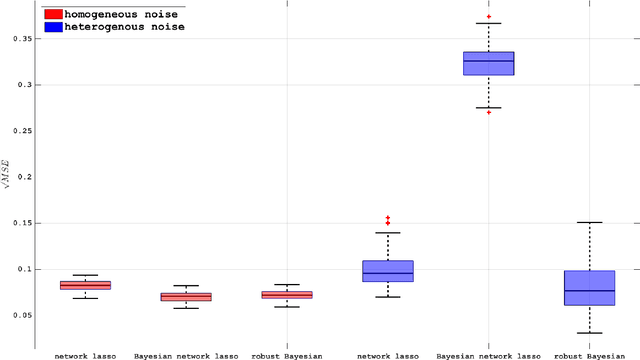
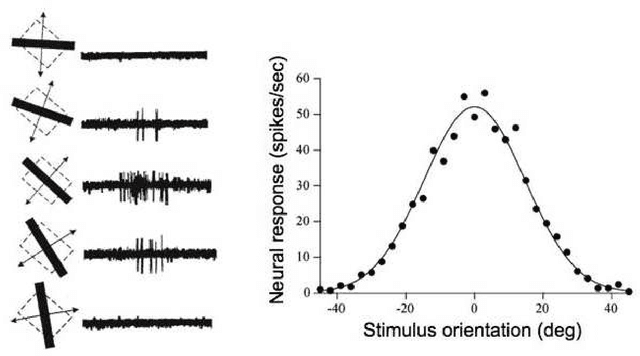
Abstract:A common analytical problem in neuroscience is the interpretation of neural activity with respect to sensory input or behavioral output. This is typically achieved by regressing measured neural activity against known stimuli or behavioral variables to produce a "tuning function" for each neuron. Unfortunately, because this approach handles neurons individually, it cannot take advantage of simultaneous measurements from spatially adjacent neurons that often have similar tuning properties. On the other hand, sharing information between adjacent neurons can errantly degrade estimates of tuning functions across space if there are sharp discontinuities in tuning between nearby neurons. In this paper, we develop a computationally efficient block Gibbs sampler that effectively pools information between neurons to de-noise tuning function estimates while simultaneously preserving sharp discontinuities that might exist in the organization of tuning across space. This method is fully Bayesian and its computational cost per iteration scales sub-quadratically with total parameter dimensionality. We demonstrate the robustness and scalability of this approach by applying it to both real and synthetic datasets. In particular, an application to data from the spinal cord illustrates that the proposed methods can dramatically decrease the experimental time required to accurately estimate tuning functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge