Error bounds in estimating the out-of-sample prediction error using leave-one-out cross validation in high-dimensions
Paper and Code
Mar 03, 2020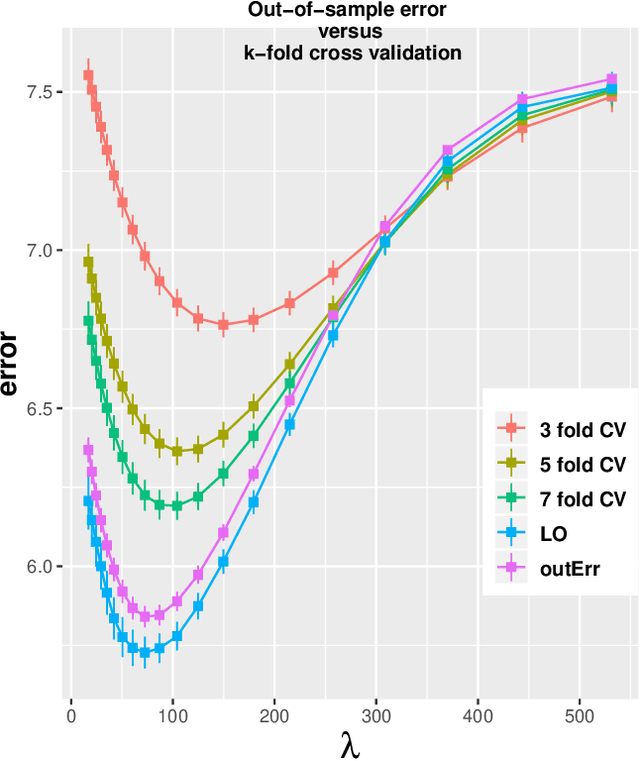
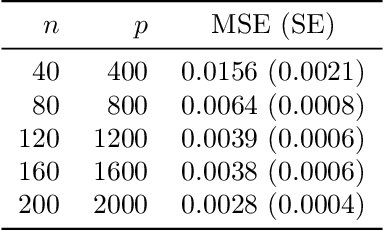
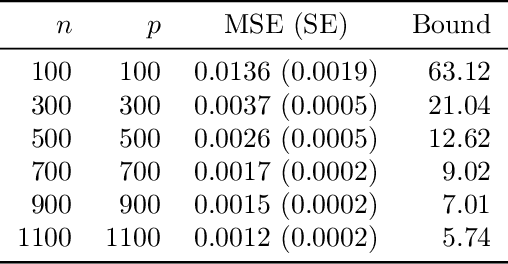
We study the problem of out-of-sample risk estimation in the high dimensional regime where both the sample size $n$ and number of features $p$ are large, and $n/p$ can be less than one. Extensive empirical evidence confirms the accuracy of leave-one-out cross validation (LO) for out-of-sample risk estimation. Yet, a unifying theoretical evaluation of the accuracy of LO in high-dimensional problems has remained an open problem. This paper aims to fill this gap for penalized regression in the generalized linear family. With minor assumptions about the data generating process, and without any sparsity assumptions on the regression coefficients, our theoretical analysis obtains finite sample upper bounds on the expected squared error of LO in estimating the out-of-sample error. Our bounds show that the error goes to zero as $n,p \rightarrow \infty$, even when the dimension $p$ of the feature vectors is comparable with or greater than the sample size $n$. One technical advantage of the theory is that it can be used to clarify and connect some results from the recent literature on scalable approximate LO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge