A Geometric Perspective for High-Dimensional Multiplex Graphs

High-dimensional multiplex graphs are characterized by their high number of complementary and divergent dimensions. The existence of multiple hierarchical latent relations between the graph dimensions poses significant challenges to embedding methods. In particular, the geometric distortions that might occur in the representational space have been overlooked in the literature. This work studies the problem of high-dimensional multiplex graph embedding from a geometric perspective. We find that the node representations reside on highly curved manifolds, thus rendering their exploitation more challenging for downstream tasks. Moreover, our study reveals that increasing the number of graph dimensions can cause further distortions to the highly curved manifolds. To address this problem, we propose a novel multiplex graph embedding method that harnesses hierarchical dimension embedding and Hyperbolic Graph Neural Networks. The proposed approach hierarchically extracts hyperbolic node representations that reside on Riemannian manifolds while gradually learning fewer and more expressive latent dimensions of the multiplex graph. Experimental results on real-world high-dimensional multiplex graphs show that the synergy between hierarchical and hyperbolic embeddings incurs much fewer geometric distortions and brings notable improvements over state-of-the-art approaches on downstream tasks.

Hierarchical Aggregations for High-Dimensional Multiplex Graph Embedding

We investigate the problem of multiplex graph embedding, that is, graphs in which nodes interact through multiple types of relations (dimensions). In recent years, several methods have been developed to address this problem. However, the need for more effective and specialized approaches grows with the production of graph data with diverse characteristics. In particular, real-world multiplex graphs may exhibit a high number of dimensions, making it difficult to construct a single consensus representation. Furthermore, important information can be hidden in complex latent structures scattered in multiple dimensions. To address these issues, we propose HMGE, a novel embedding method based on hierarchical aggregation for high-dimensional multiplex graphs. Hierarchical aggregation consists of learning a hierarchical combination of the graph dimensions and refining the embeddings at each hierarchy level. Non-linear combinations are computed from previous ones, thus uncovering complex information and latent structures hidden in the multiplex graph dimensions. Moreover, we leverage mutual information maximization between local patches and global summaries to train the model without supervision. This allows to capture of globally relevant information present in diverse locations of the graph. Detailed experiments on synthetic and real-world data illustrate the suitability of our approach to downstream supervised tasks, including link prediction and node classification.

A Deep Learning Based Cost Model for Automatic Code Optimization

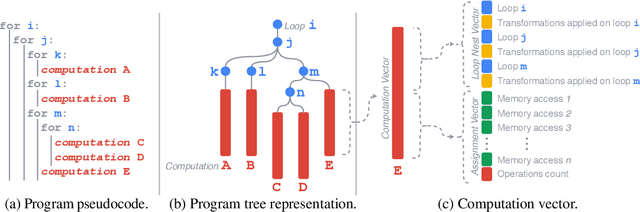
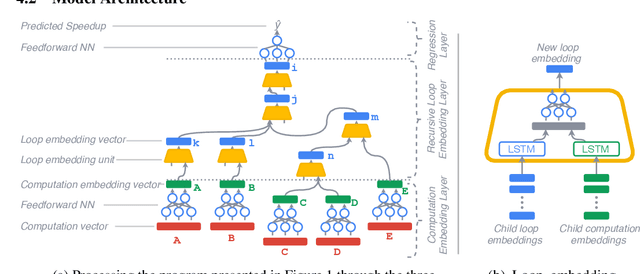
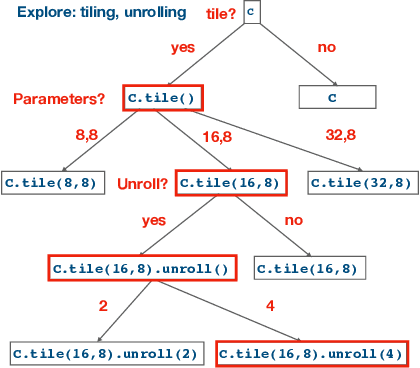
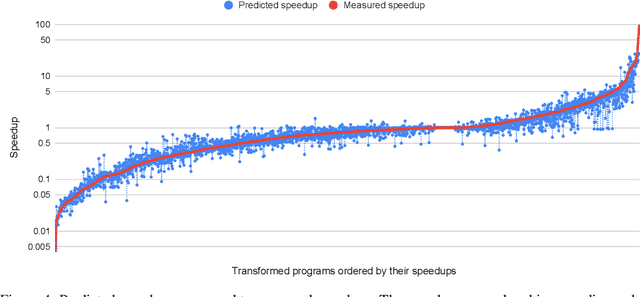
Enabling compilers to automatically optimize code has been a longstanding goal for the compiler community. Efficiently solving this problem requires using precise cost models. These models predict whether applying a sequence of code transformations reduces the execution time of the program. Building an analytical cost model to do so is hard in modern x86 architectures due to the complexity of the microarchitecture. In this paper, we present a novel deep learning based cost model for automatic code optimization. This model was integrated in a search method and implemented in the Tiramisu compiler to select the best code transformations. The input of the proposed model is a set of simple features representing the unoptimized code and a sequence of code transformations. The model predicts the speedup expected when the code transformations are applied. Unlike previous models, the proposed one works on full programs and does not rely on any heavy feature engineering. The proposed model has only 16% of mean absolute percentage error in predicting speedups on full programs. The proposed model enables Tiramisu to automatically find code transformations that match or are better than state-of-the-art compilers without requiring the same level of heavy feature engineering required by those compilers.

TIRAMISU: A Polyhedral Compiler for Dense and Sparse Deep Learning

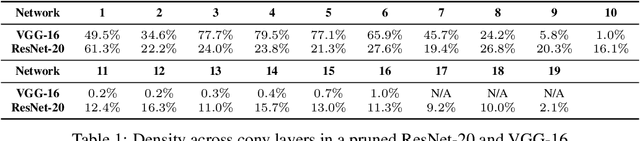
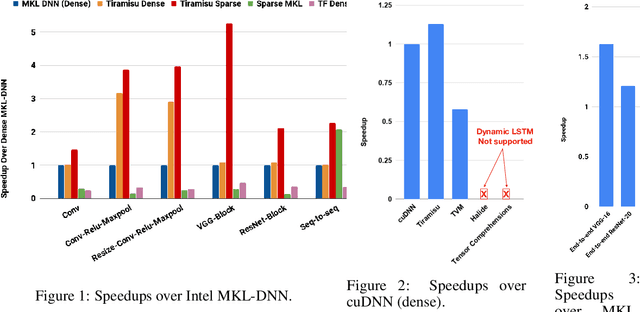
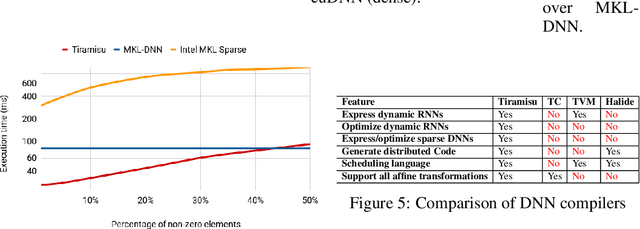
In this paper, we demonstrate a compiler that can optimize sparse and recurrent neural networks, both of which are currently outside of the scope of existing neural network compilers (sparse neural networks here stand for networks that can be accelerated with sparse tensor algebra techniques). Our demonstration includes a mapping of sparse and recurrent neural networks to the polyhedral model along with an implementation of our approach in TIRAMISU, our state-of-the-art polyhedral compiler. We evaluate our approach on a set of deep learning benchmarks and compare our results with hand-optimized industrial libraries. Our results show that our approach at least matches Intel MKL-DNN and in some cases outperforms it by 5x (on multicore-CPUs).