Investigating Pre-trained Language Models on Cross-Domain Datasets, a Step Closer to General AI

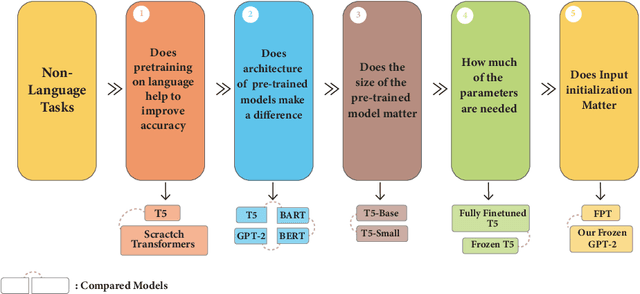
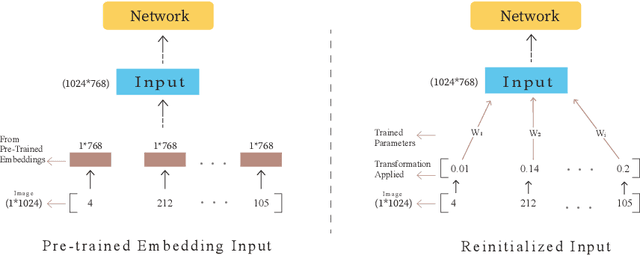
Pre-trained language models have recently emerged as a powerful tool for fine-tuning a variety of language tasks. Ideally, when models are pre-trained on large amount of data, they are expected to gain implicit knowledge. In this paper, we investigate the ability of pre-trained language models to generalize to different non-language tasks. In particular, we test them on tasks from different domains such as computer vision, reasoning on hierarchical data, and protein fold prediction. The four pre-trained models that we used, T5, BART, BERT, and GPT-2 achieve outstanding results. They all have similar performance and they outperform transformers that are trained from scratch by a large margin. For instance, pre-trained language models perform better on the Listops dataset, with an average accuracy of 58.7\%, compared to transformers trained from scratch, which have an average accuracy of 29.0\%. The significant improvement demonstrated across three types of datasets suggests that pre-training on language helps the models to acquire general knowledge, bringing us a step closer to general AI. We also showed that reducing the number of parameters in pre-trained language models does not have a great impact as the performance drops slightly when using T5-Small instead of T5-Base. In fact, when using only 2\% of the parameters, we achieved a great improvement compared to training from scratch. Finally, in contrast to prior work, we find out that using pre-trained embeddings for the input layer is necessary to achieve the desired results.

Opening the Black Box: Analyzing Attention Weights and Hidden States in Pre-trained Language Models for Non-language Tasks

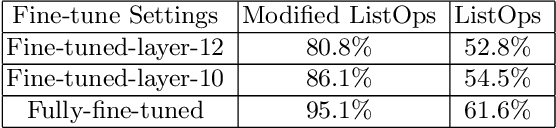
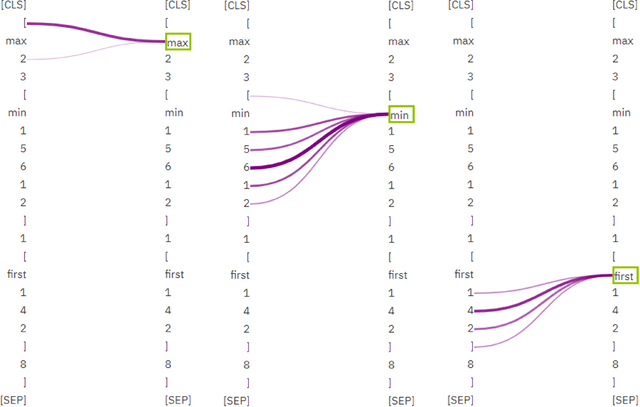
Investigating deep learning language models has always been a significant research area due to the ``black box" nature of most advanced models. With the recent advancements in pre-trained language models based on transformers and their increasing integration into daily life, addressing this issue has become more pressing. In order to achieve an explainable AI model, it is essential to comprehend the procedural steps involved and compare them with human thought processes. Thus, in this paper, we use simple, well-understood non-language tasks to explore these models' inner workings. Specifically, we apply a pre-trained language model to constrained arithmetic problems with hierarchical structure, to analyze their attention weight scores and hidden states. The investigation reveals promising results, with the model addressing hierarchical problems in a moderately structured manner, similar to human problem-solving strategies. Additionally, by inspecting the attention weights layer by layer, we uncover an unconventional finding that layer 10, rather than the model's final layer, is the optimal layer to unfreeze for the least parameter-intensive approach to fine-tune the model. We support these findings with entropy analysis and token embeddings similarity analysis. The attention analysis allows us to hypothesize that the model can generalize to longer sequences in ListOps dataset, a conclusion later confirmed through testing on sequences longer than those in the training set. Lastly, by utilizing a straightforward task in which the model predicts the winner of a Tic Tac Toe game, we identify limitations in attention analysis, particularly its inability to capture 2D patterns.

Grounding Psychological Shape Space in Convolutional Neural Networks

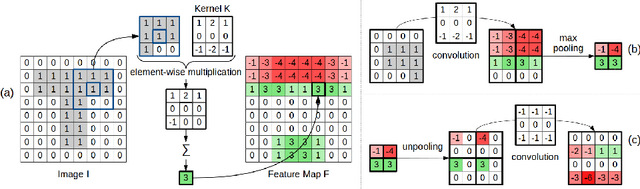
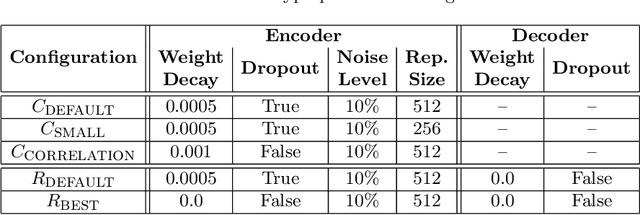
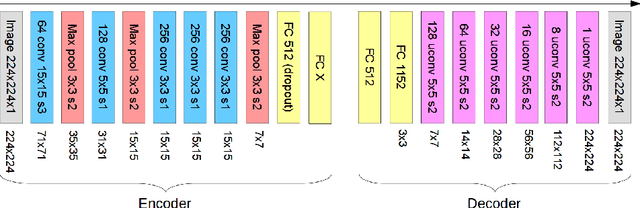
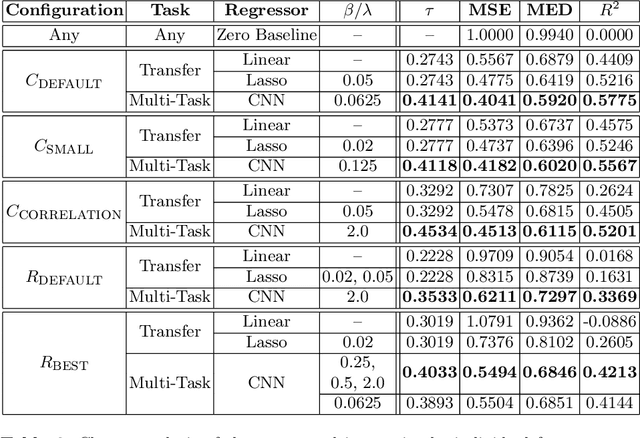
Shape information is crucial for human perception and cognition, and should therefore also play a role in cognitive AI systems. We employ the interdisciplinary framework of conceptual spaces, which proposes a geometric representation of conceptual knowledge through low-dimensional interpretable similarity spaces. These similarity spaces are often based on psychological dissimilarity ratings for a small set of stimuli, which are then transformed into a spatial representation by a technique called multidimensional scaling. Unfortunately, this approach is incapable of generalizing to novel stimuli. In this paper, we use convolutional neural networks to learn a generalizable mapping between perceptual inputs (pixels of grayscale line drawings) and a recently proposed psychological similarity space for the shape domain. We investigate different network architectures (classification network vs. autoencoder) and different training regimes (transfer learning vs. multi-task learning). Our results indicate that a classification-based multi-task learning scenario yields the best results, but that its performance is relatively sensitive to the dimensionality of the similarity space.

Fast Concept Mapping: The Emergence of Human Abilities in Artificial Neural Networks when Learning Embodied and Self-Supervised

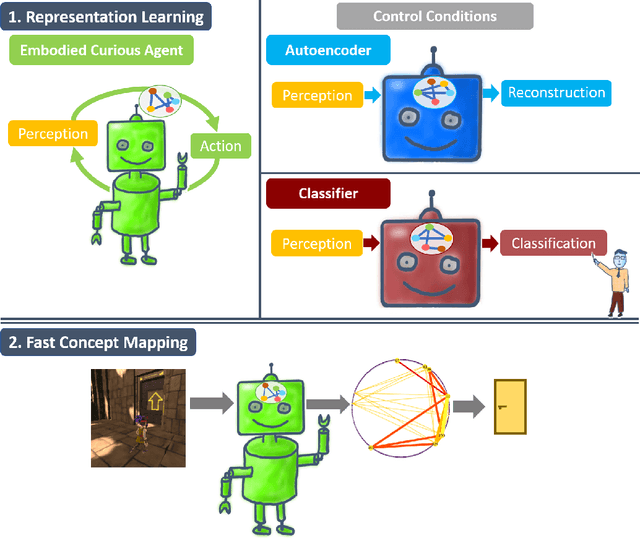
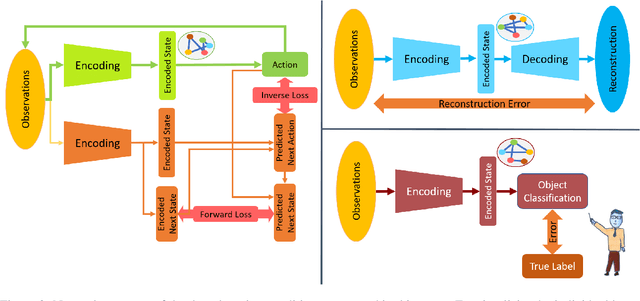
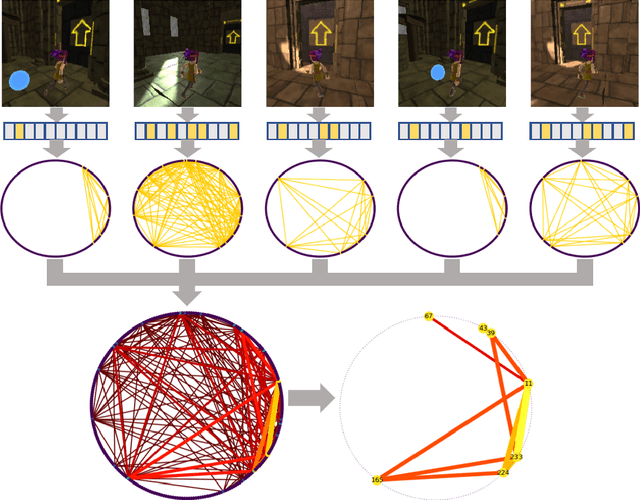
Most artificial neural networks used for object detection and recognition are trained in a fully supervised setup. This is not only very resource consuming as it requires large data sets of labeled examples but also very different from how humans learn. We introduce a setup in which an artificial agent first learns in a simulated world through self-supervised exploration. Following this, the representations learned through interaction with the world can be used to associate semantic concepts such as different types of doors. To do this, we use a method we call fast concept mapping which uses correlated firing patterns of neurons to define and detect semantic concepts. This association works instantaneous with very few labeled examples, similar to what we observe in humans in a phenomenon called fast mapping. Strikingly, this method already identifies objects with as little as one labeled example which highlights the quality of the encoding learned self-supervised through embodiment using curiosity-driven exploration. It therefor presents a feasible strategy for learning concepts without much supervision and shows that through pure interaction with the world meaningful representations of an environment can be learned.

Generalizing Psychological Similarity Spaces to Unseen Stimuli

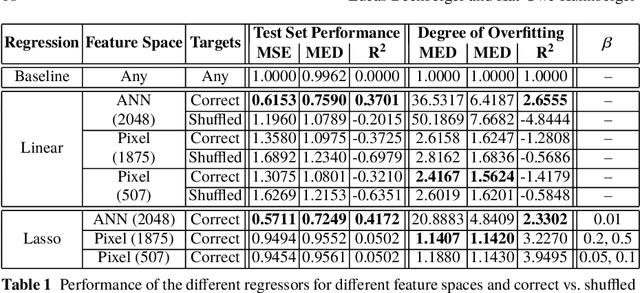
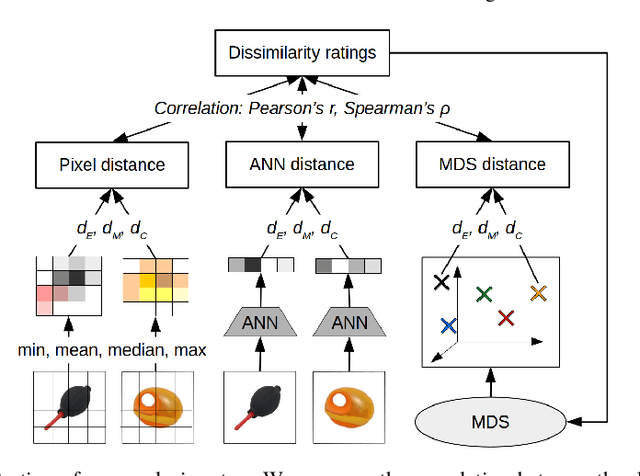
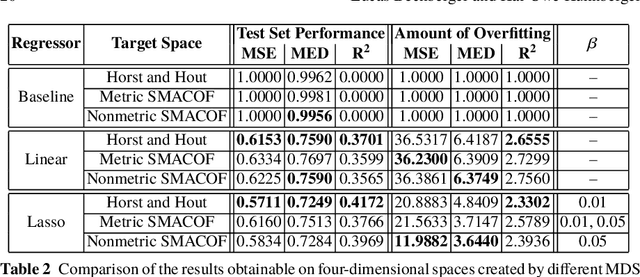
The cognitive framework of conceptual spaces proposes to represent concepts as regions in psychological similarity spaces. These similarity spaces are typically obtained through multidimensional scaling (MDS), which converts human dissimilarity ratings for a fixed set of stimuli into a spatial representation. One can distinguish metric MDS (which assumes that the dissimilarity ratings are interval or ratio scaled) from nonmetric MDS (which only assumes an ordinal scale). In our first study, we show that despite its additional assumptions, metric MDS does not necessarily yield better solutions than nonmetric MDS. In this chapter, we furthermore propose to learn a mapping from raw stimuli into the similarity space using artificial neural networks (ANNs) in order to generalize the similarity space to unseen inputs. In our second study, we show that a linear regression from the activation vectors of a convolutional ANN to similarity spaces obtained by MDS can be successful and that the results are sensitive to the number of dimensions of the similarity space.

A Comprehensive Implementation of Conceptual Spaces

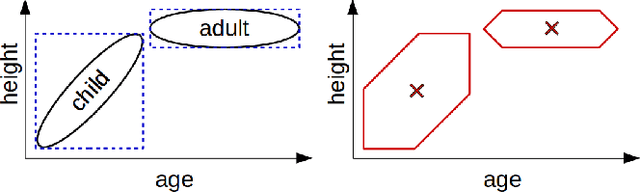
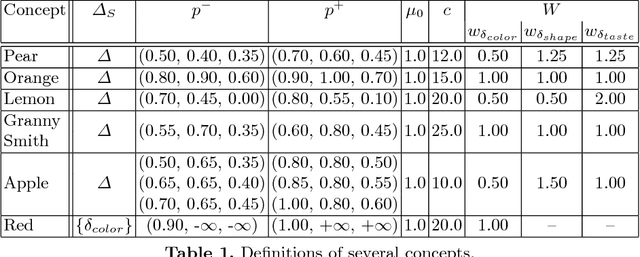
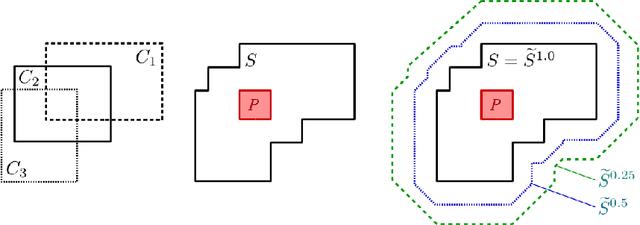
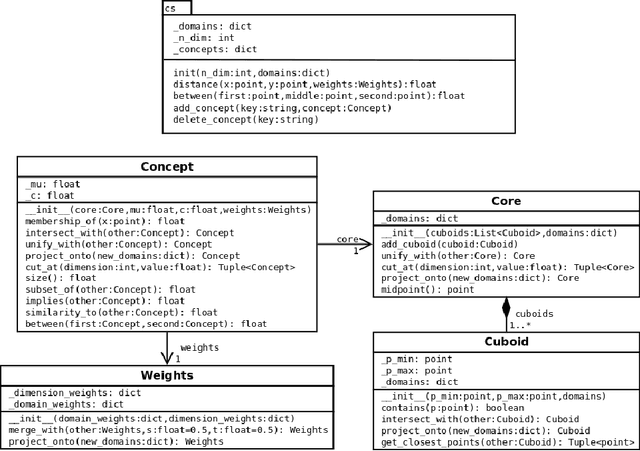
The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points and concepts are represented by regions in a (potentially) high-dimensional space. Based on our recent formalization, we present a comprehensive implementation of the conceptual spaces framework that is not only capable of representing concepts with inter-domain correlations, but that also offers a variety of operations on these concepts.

Formal Ways for Measuring Relations between Concepts in Conceptual Spaces

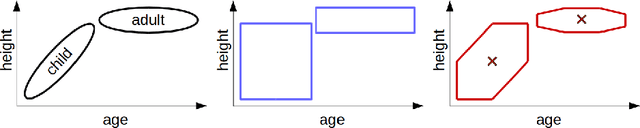
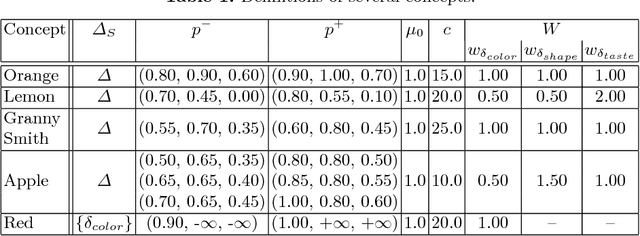
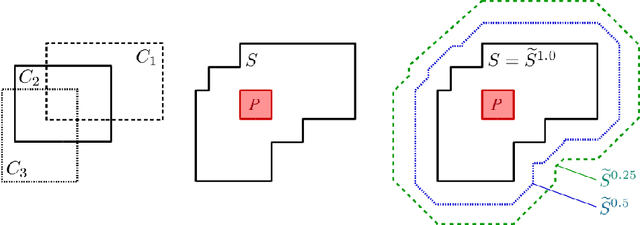
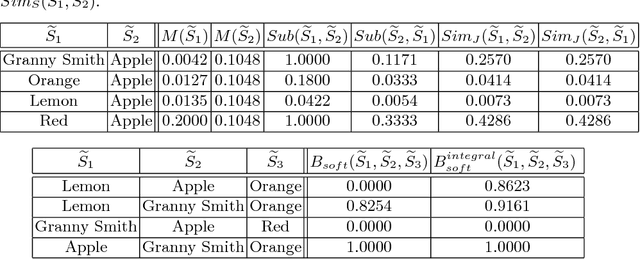
The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a high-dimensional space and concepts are represented by regions in this space. In this article, we extend our recent mathematical formalization of this framework by providing quantitative mathematical definitions for measuring relations between concepts: We develop formal ways for computing concept size, subsethood, implication, similarity, and betweenness. This considerably increases the representational capabilities of our formalization and makes it the most thorough and comprehensive formalization of conceptual spaces developed so far.

Formalized Conceptual Spaces with a Geometric Representation of Correlations

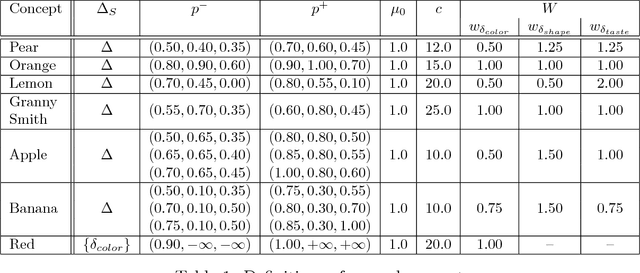
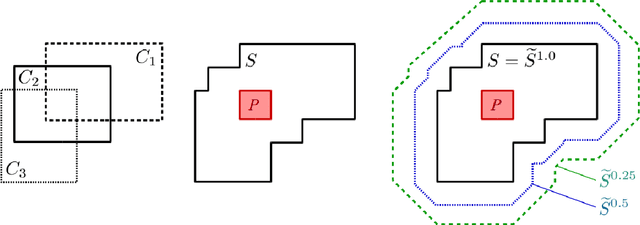
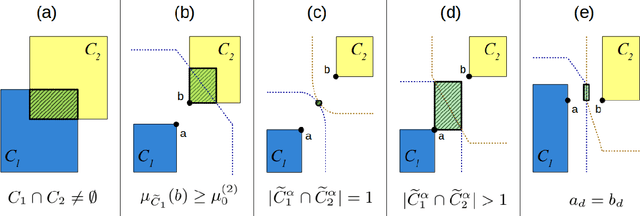
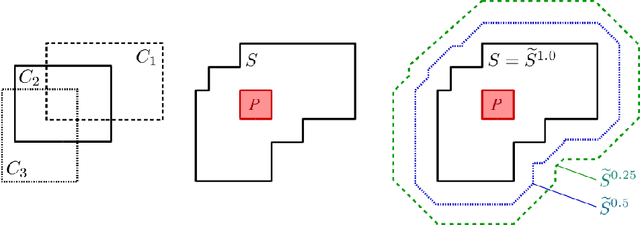
The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a similarity space and concepts are represented by convex regions in this space. After pointing out a problem with the convexity requirement, we propose a formalization of conceptual spaces based on fuzzy star-shaped sets. Our formalization uses a parametric definition of concepts and extends the original framework by adding means to represent correlations between different domains in a geometric way. Moreover, we define various operations for our formalization, both for creating new concepts from old ones and for measuring relations between concepts. We present an illustrative toy-example and sketch a research project on concept formation that is based on both our formalization and its implementation.

Measuring Relations Between Concepts In Conceptual Spaces

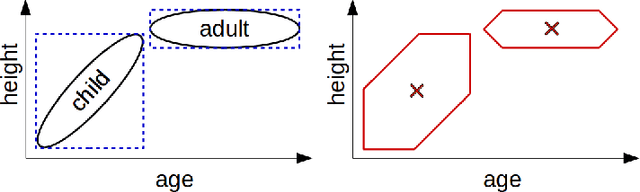
The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a high-dimensional space and concepts are represented by regions in this space. Our recent mathematical formalization of this framework is capable of representing correlations between different domains in a geometric way. In this paper, we extend our formalization by providing quantitative mathematical definitions for the notions of concept size, subsethood, implication, similarity, and betweenness. This considerably increases the representational power of our formalization by introducing measurable ways of describing relations between concepts.

Towards Grounding Conceptual Spaces in Neural Representations

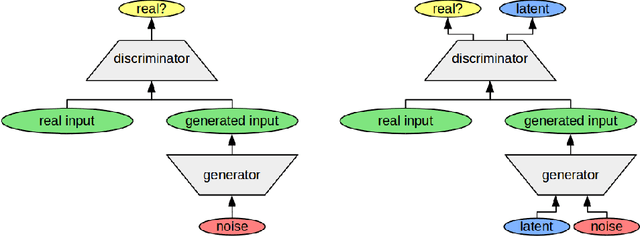
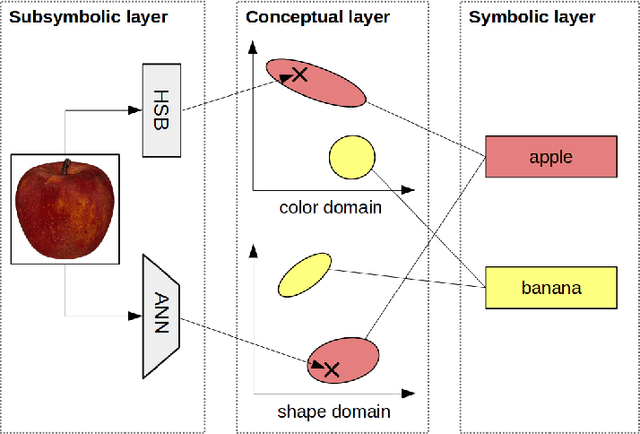
The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. It aims at bridging the gap between symbolic and subsymbolic processing. Instances are represented by points in a high-dimensional space and concepts are represented by convex regions in this space. In this paper, we present our approach towards grounding the dimensions of a conceptual space in latent spaces learned by an InfoGAN from unlabeled data.