Lucas Bechberger
Grounding Psychological Shape Space in Convolutional Neural Networks
Nov 16, 2021
Abstract:Shape information is crucial for human perception and cognition, and should therefore also play a role in cognitive AI systems. We employ the interdisciplinary framework of conceptual spaces, which proposes a geometric representation of conceptual knowledge through low-dimensional interpretable similarity spaces. These similarity spaces are often based on psychological dissimilarity ratings for a small set of stimuli, which are then transformed into a spatial representation by a technique called multidimensional scaling. Unfortunately, this approach is incapable of generalizing to novel stimuli. In this paper, we use convolutional neural networks to learn a generalizable mapping between perceptual inputs (pixels of grayscale line drawings) and a recently proposed psychological similarity space for the shape domain. We investigate different network architectures (classification network vs. autoencoder) and different training regimes (transfer learning vs. multi-task learning). Our results indicate that a classification-based multi-task learning scenario yields the best results, but that its performance is relatively sensitive to the dimensionality of the similarity space.
Generalizing Psychological Similarity Spaces to Unseen Stimuli
Aug 25, 2019
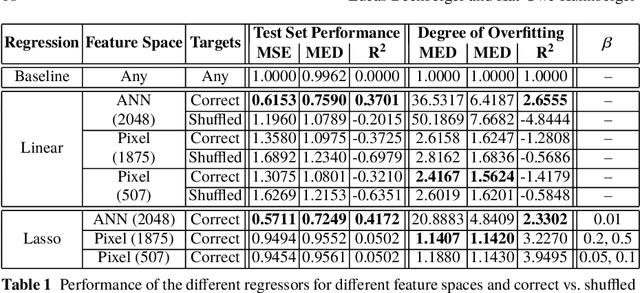
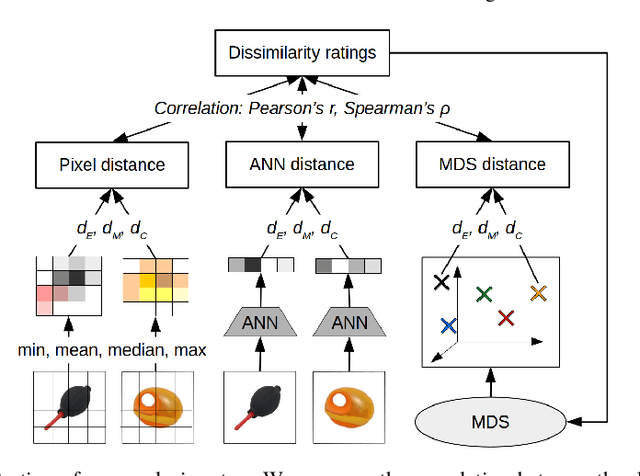
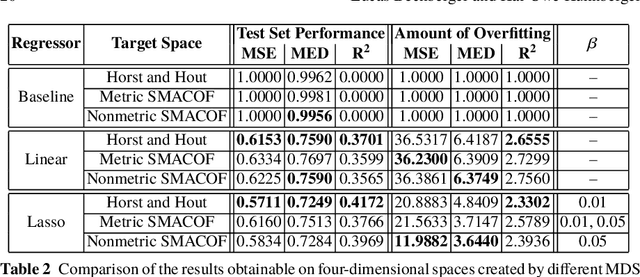
Abstract:The cognitive framework of conceptual spaces proposes to represent concepts as regions in psychological similarity spaces. These similarity spaces are typically obtained through multidimensional scaling (MDS), which converts human dissimilarity ratings for a fixed set of stimuli into a spatial representation. One can distinguish metric MDS (which assumes that the dissimilarity ratings are interval or ratio scaled) from nonmetric MDS (which only assumes an ordinal scale). In our first study, we show that despite its additional assumptions, metric MDS does not necessarily yield better solutions than nonmetric MDS. In this chapter, we furthermore propose to learn a mapping from raw stimuli into the similarity space using artificial neural networks (ANNs) in order to generalize the similarity space to unseen inputs. In our second study, we show that a linear regression from the activation vectors of a convolutional ANN to similarity spaces obtained by MDS can be successful and that the results are sensitive to the number of dimensions of the similarity space.
A Comprehensive Implementation of Conceptual Spaces
Apr 23, 2018
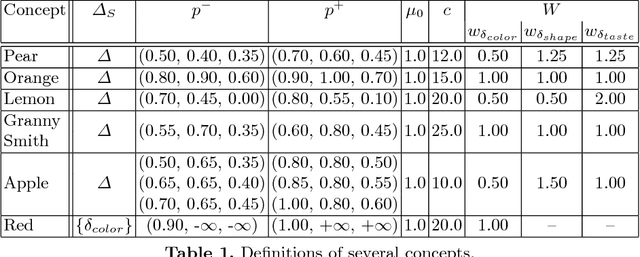
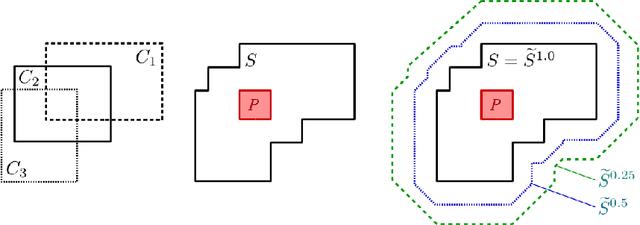
Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points and concepts are represented by regions in a (potentially) high-dimensional space. Based on our recent formalization, we present a comprehensive implementation of the conceptual spaces framework that is not only capable of representing concepts with inter-domain correlations, but that also offers a variety of operations on these concepts.
Mapping Images to Psychological Similarity Spaces Using Neural Networks
Apr 20, 2018



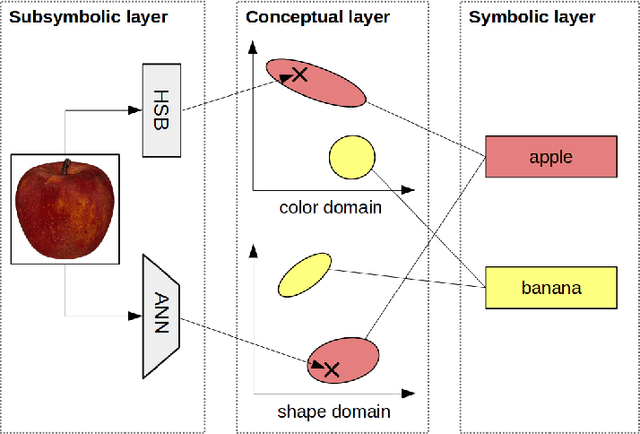
Abstract:The cognitive framework of conceptual spaces bridges the gap between symbolic and subsymbolic AI by proposing an intermediate conceptual layer where knowledge is represented geometrically. There are two main approaches for obtaining the dimensions of this conceptual similarity space: using similarity ratings from psychological experiments and using machine learning techniques. In this paper, we propose a combination of both approaches by using psychologically derived similarity ratings to constrain the machine learning process. This way, a mapping from stimuli to conceptual spaces can be learned that is both supported by psychological data and allows generalization to unseen stimuli. The results of a first feasibility study support our proposed approach.
Formal Ways for Measuring Relations between Concepts in Conceptual Spaces
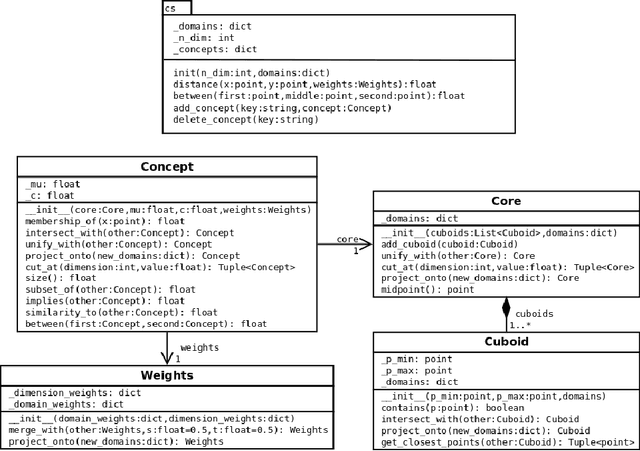
Apr 06, 2018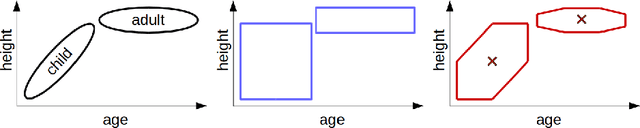
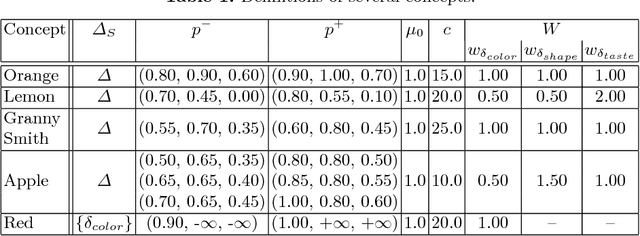
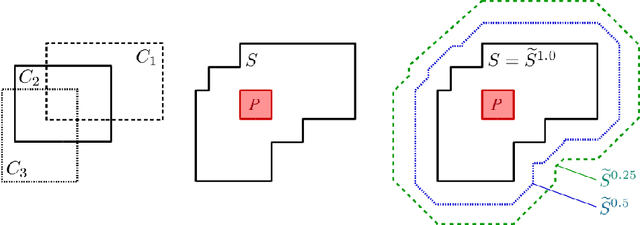
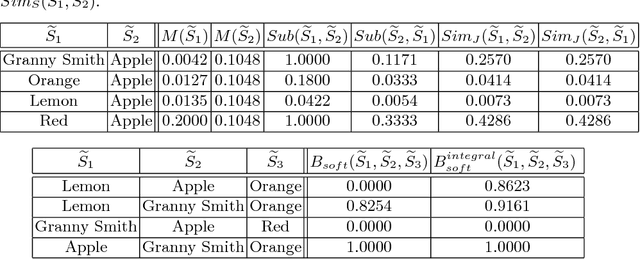
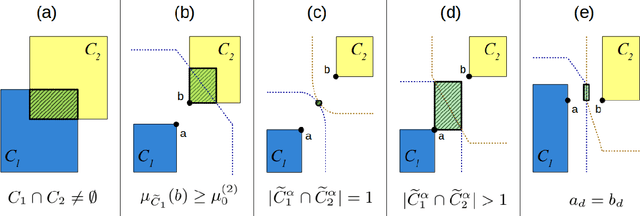
Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a high-dimensional space and concepts are represented by regions in this space. In this article, we extend our recent mathematical formalization of this framework by providing quantitative mathematical definitions for measuring relations between concepts: We develop formal ways for computing concept size, subsethood, implication, similarity, and betweenness. This considerably increases the representational capabilities of our formalization and makes it the most thorough and comprehensive formalization of conceptual spaces developed so far.
Formalized Conceptual Spaces with a Geometric Representation of Correlations
Jan 11, 2018
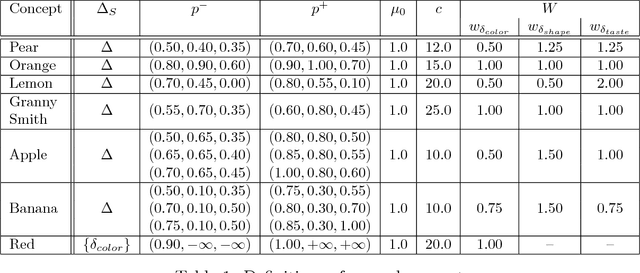
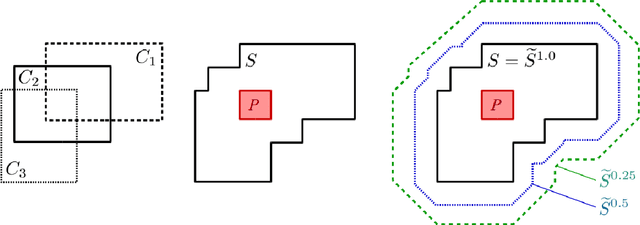
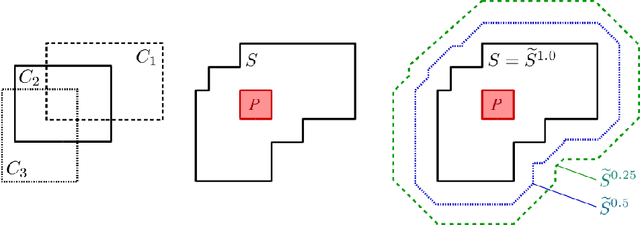
Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a similarity space and concepts are represented by convex regions in this space. After pointing out a problem with the convexity requirement, we propose a formalization of conceptual spaces based on fuzzy star-shaped sets. Our formalization uses a parametric definition of concepts and extends the original framework by adding means to represent correlations between different domains in a geometric way. Moreover, we define various operations for our formalization, both for creating new concepts from old ones and for measuring relations between concepts. We present an illustrative toy-example and sketch a research project on concept formation that is based on both our formalization and its implementation.
Measuring Relations Between Concepts In Conceptual Spaces
Dec 06, 2017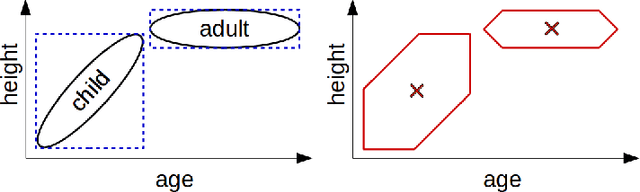


Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a high-dimensional space and concepts are represented by regions in this space. Our recent mathematical formalization of this framework is capable of representing correlations between different domains in a geometric way. In this paper, we extend our formalization by providing quantitative mathematical definitions for the notions of concept size, subsethood, implication, similarity, and betweenness. This considerably increases the representational power of our formalization by introducing measurable ways of describing relations between concepts.
Towards Grounding Conceptual Spaces in Neural Representations
Nov 21, 2017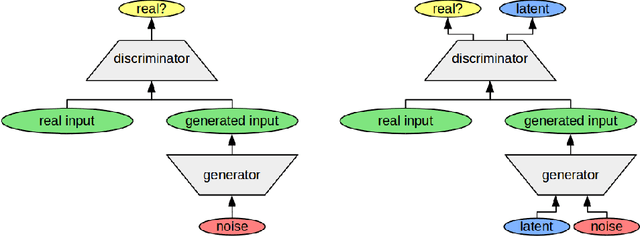
Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. It aims at bridging the gap between symbolic and subsymbolic processing. Instances are represented by points in a high-dimensional space and concepts are represented by convex regions in this space. In this paper, we present our approach towards grounding the dimensions of a conceptual space in latent spaces learned by an InfoGAN from unlabeled data.
The Size of a Hyperball in a Conceptual Space
Sep 22, 2017
Abstract:The cognitive framework of conceptual spaces [3] provides geometric means for representing knowledge. A conceptual space is a high-dimensional space whose dimensions are partitioned into so-called domains. Within each domain, the Euclidean metric is used to compute distances. Distances in the overall space are computed by applying the Manhattan metric to the intra-domain distances. Instances are represented as points in this space and concepts are represented by regions. In this paper, we derive a formula for the size of a hyperball under the combined metric of a conceptual space. One can think of such a hyperball as the set of all points having a certain minimal similarity to the hyperball's center.
A Thorough Formalization of Conceptual Spaces
Sep 21, 2017

Abstract:The highly influential framework of conceptual spaces provides a geometric way of representing knowledge. Instances are represented by points in a high-dimensional space and concepts are represented by convex regions in this space. After pointing out a problem with the convexity requirement, we propose a formalization of conceptual spaces based on fuzzy star-shaped sets. Our formalization uses a parametric definition of concepts and extends the original framework by adding means to represent correlations between different domains in a geometric way. Moreover, we define computationally efficient operations on concepts (intersection, union, and projection onto a subspace) and show that these operations can support both learning and reasoning processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge