Residual Networks as Nonlinear Systems: Stability Analysis using Linearization

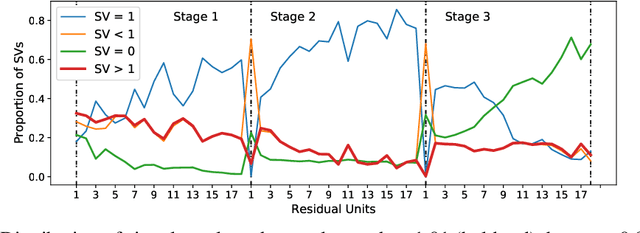
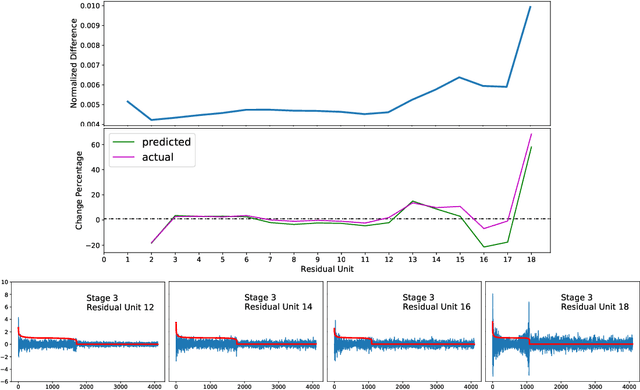
We regard pre-trained residual networks (ResNets) as nonlinear systems and use linearization, a common method used in the qualitative analysis of nonlinear systems, to understand the behavior of the networks under small perturbations of the input images. We work with ResNet-56 and ResNet-110 trained on the CIFAR-10 data set. We linearize these networks at the level of residual units and network stages, and the singular value decomposition is used in the stability analysis of these components. It is found that most of the singular values of the linearizations of residual units are 1 and, in spite of the fact that the linearizations depend directly on the activation maps, the singular values differ only slightly for different input images. However, adjusting the scaling of the skip connection or the values of the weights in a residual unit has a significant impact on the singular value distributions. Inspection of how random and adversarial perturbations of input images propagate through the network reveals that there is a dramatic jump in the magnitude of adversarial perturbations towards the end of the final stage of the network that is not present in the case of random perturbations. We attempt to gain a better understanding of this phenomenon by projecting the perturbations onto singular vectors of the linearizations of the residual units.

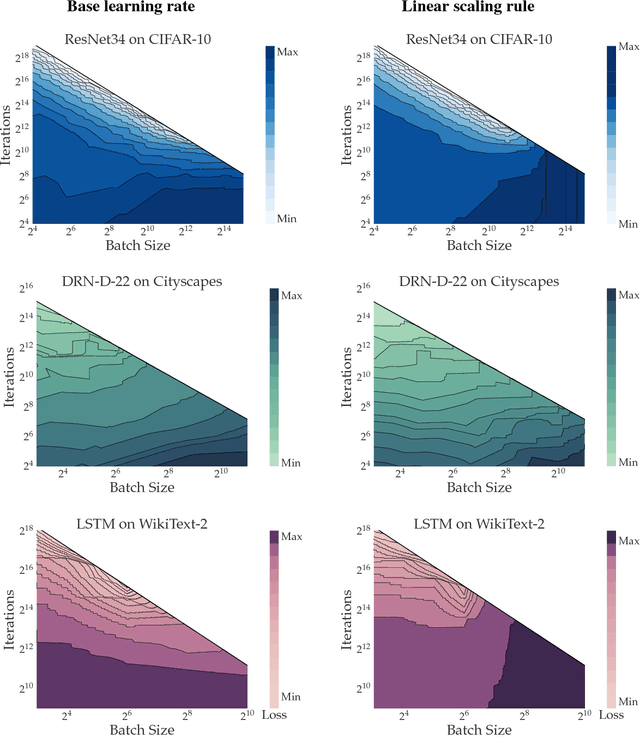
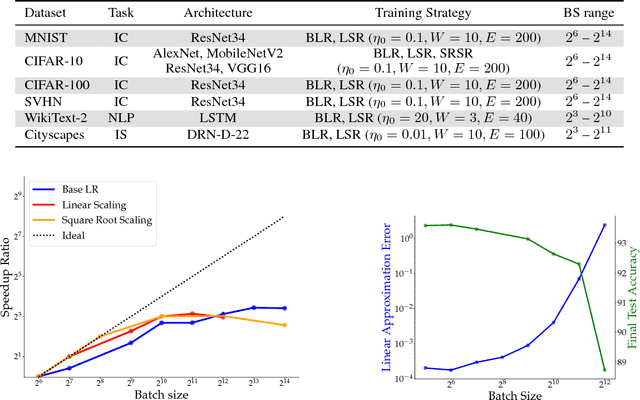
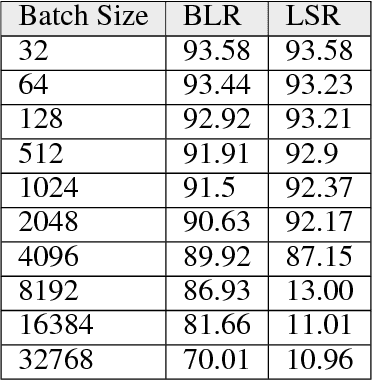
On the Computational Inefficiency of Large Batch Sizes for Stochastic Gradient Descent

Increasing the mini-batch size for stochastic gradient descent offers significant opportunities to reduce wall-clock training time, but there are a variety of theoretical and systems challenges that impede the widespread success of this technique. We investigate these issues, with an emphasis on time to convergence and total computational cost, through an extensive empirical analysis of network training across several architectures and problem domains, including image classification, image segmentation, and language modeling. Although it is common practice to increase the batch size in order to fully exploit available computational resources, we find a substantially more nuanced picture. Our main finding is that across a wide range of network architectures and problem domains, increasing the batch size beyond a certain point yields no decrease in wall-clock time to convergence for \emph{either} train or test loss. This batch size is usually substantially below the capacity of current systems. We show that popular training strategies for large batch size optimization begin to fail before we can populate all available compute resources, and we show that the point at which these methods break down depends more on attributes like model architecture and data complexity than it does directly on the size of the dataset.