On the Computational Inefficiency of Large Batch Sizes for Stochastic Gradient Descent
Paper and Code
Nov 30, 2018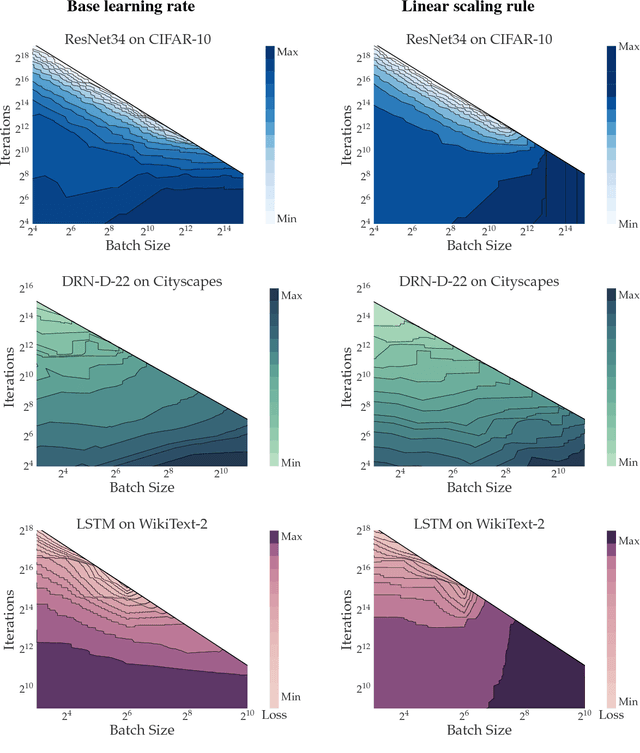
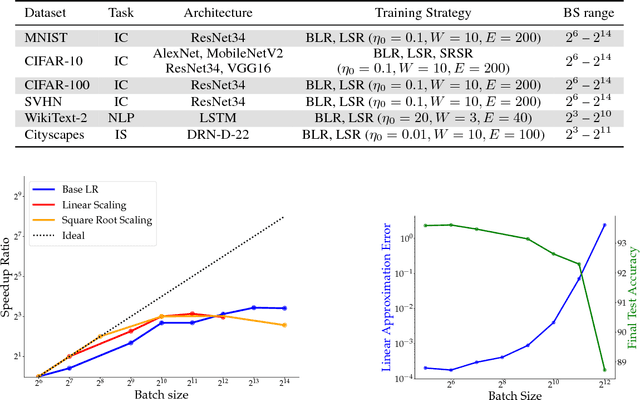
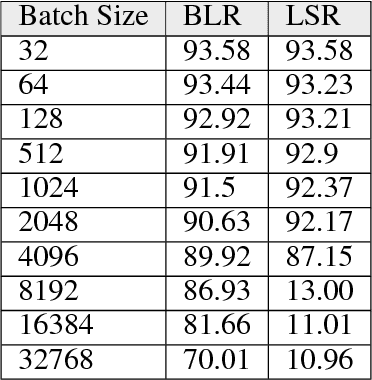

Increasing the mini-batch size for stochastic gradient descent offers significant opportunities to reduce wall-clock training time, but there are a variety of theoretical and systems challenges that impede the widespread success of this technique. We investigate these issues, with an emphasis on time to convergence and total computational cost, through an extensive empirical analysis of network training across several architectures and problem domains, including image classification, image segmentation, and language modeling. Although it is common practice to increase the batch size in order to fully exploit available computational resources, we find a substantially more nuanced picture. Our main finding is that across a wide range of network architectures and problem domains, increasing the batch size beyond a certain point yields no decrease in wall-clock time to convergence for \emph{either} train or test loss. This batch size is usually substantially below the capacity of current systems. We show that popular training strategies for large batch size optimization begin to fail before we can populate all available compute resources, and we show that the point at which these methods break down depends more on attributes like model architecture and data complexity than it does directly on the size of the dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge