Zixi Hu
Residual Networks as Nonlinear Systems: Stability Analysis using Linearization
May 31, 2019
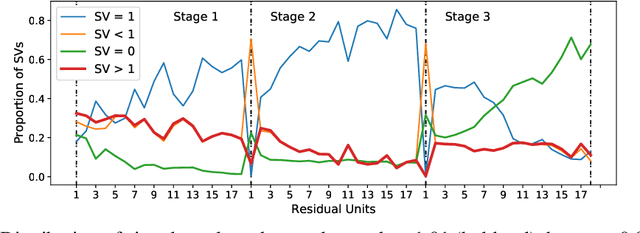

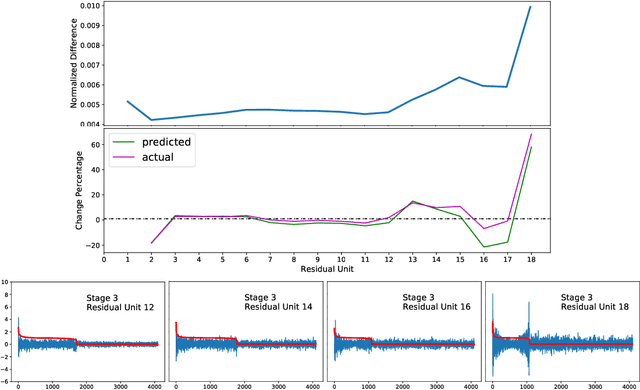
Abstract:We regard pre-trained residual networks (ResNets) as nonlinear systems and use linearization, a common method used in the qualitative analysis of nonlinear systems, to understand the behavior of the networks under small perturbations of the input images. We work with ResNet-56 and ResNet-110 trained on the CIFAR-10 data set. We linearize these networks at the level of residual units and network stages, and the singular value decomposition is used in the stability analysis of these components. It is found that most of the singular values of the linearizations of residual units are 1 and, in spite of the fact that the linearizations depend directly on the activation maps, the singular values differ only slightly for different input images. However, adjusting the scaling of the skip connection or the values of the weights in a residual unit has a significant impact on the singular value distributions. Inspection of how random and adversarial perturbations of input images propagate through the network reveals that there is a dramatic jump in the magnitude of adversarial perturbations towards the end of the final stage of the network that is not present in the case of random perturbations. We attempt to gain a better understanding of this phenomenon by projecting the perturbations onto singular vectors of the linearizations of the residual units.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge