Operational range bounding of spectroscopy models with anomaly detection

Safe operation of machine learning models requires architectures that explicitly delimit their operational ranges. We evaluate the ability of anomaly detection algorithms to provide indicators correlated with degraded model performance. By placing acceptance thresholds over such indicators, hard boundaries are formed that define the model's coverage. As a use case, we consider the extraction of exoplanetary spectra from transit light curves, specifically within the context of ESA's upcoming Ariel mission. Isolation Forests are shown to effectively identify contexts where prediction models are likely to fail. Coverage/error trade-offs are evaluated under conditions of data and concept drift. The best performance is seen when Isolation Forests model projections of the prediction model's explainability SHAP values.

Don't Pay Attention to the Noise: Learning Self-supervised Representations of Light Curves with a Denoising Time Series Transformer

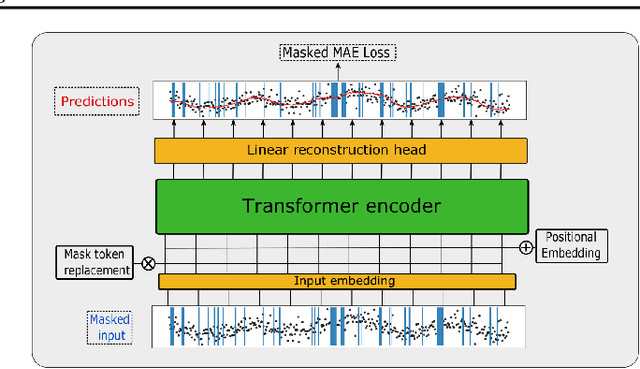
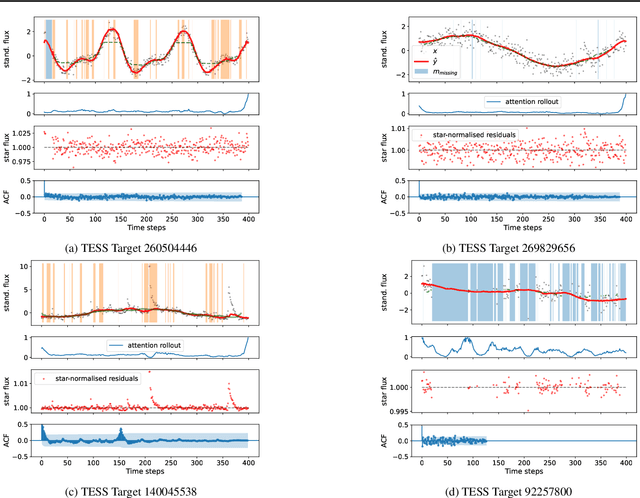
Astrophysical light curves are particularly challenging data objects due to the intensity and variety of noise contaminating them. Yet, despite the astronomical volumes of light curves available, the majority of algorithms used to process them are still operating on a per-sample basis. To remedy this, we propose a simple Transformer model -- called Denoising Time Series Transformer (DTST) -- and show that it excels at removing the noise and outliers in datasets of time series when trained with a masked objective, even when no clean targets are available. Moreover, the use of self-attention enables rich and illustrative queries into the learned representations. We present experiments on real stellar light curves from the Transiting Exoplanet Space Satellite (TESS), showing advantages of our approach compared to traditional denoising techniques.

Conservative Policy Construction Using Variational Autoencoders for Logged Data with Missing Values

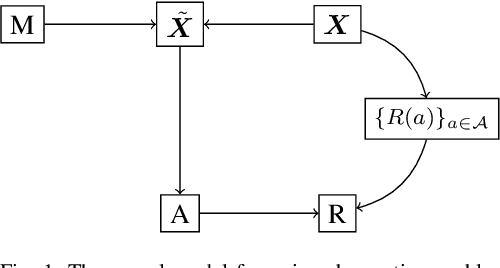
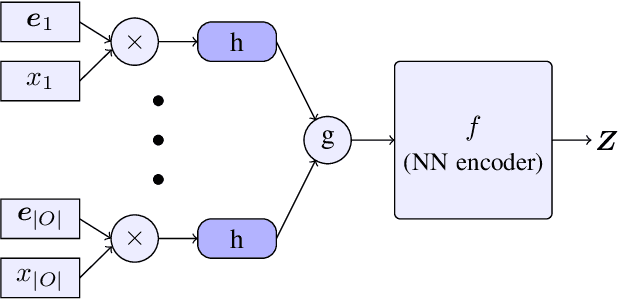
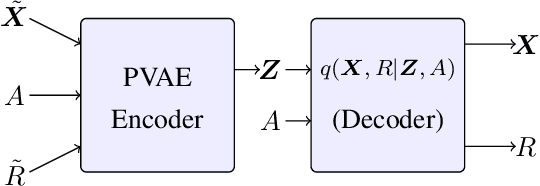
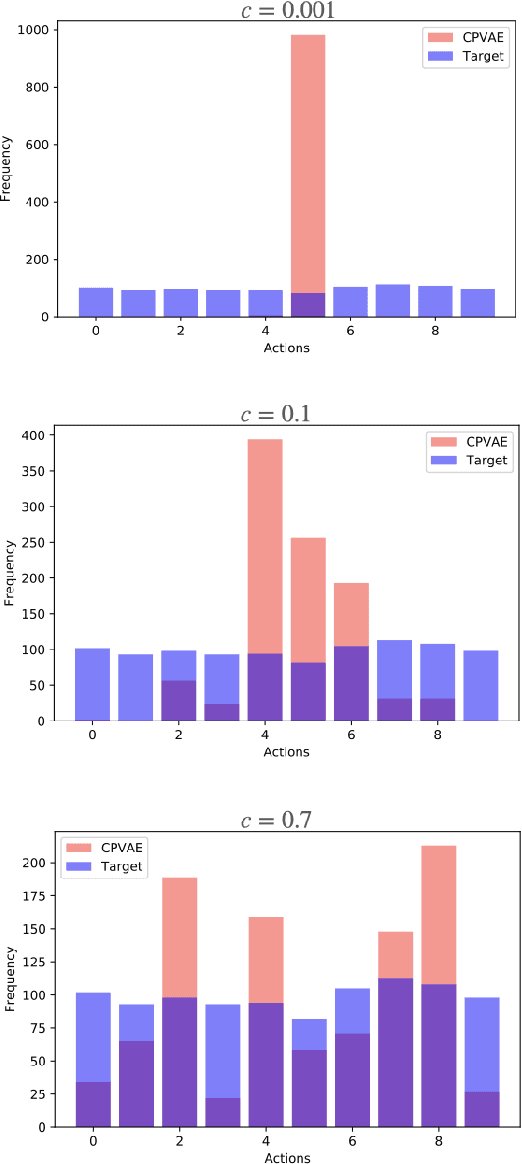
In high-stakes applications of data-driven decision making like healthcare, it is of paramount importance to learn a policy that maximizes the reward while avoiding potentially dangerous actions when there is uncertainty. There are two main challenges usually associated with this problem. Firstly, learning through online exploration is not possible due to the critical nature of such applications. Therefore, we need to resort to observational datasets with no counterfactuals. Secondly, such datasets are usually imperfect, additionally cursed with missing values in the attributes of features. In this paper, we consider the problem of constructing personalized policies using logged data when there are missing values in the attributes of features in both training and test data. The goal is to recommend an action (treatment) when $\Xt$, a degraded version of $\Xb$ with missing values, is observed. We consider three strategies for dealing with missingness. In particular, we introduce the \textit{conservative strategy} where the policy is designed to safely handle the uncertainty due to missingness. In order to implement this strategy we need to estimate posterior distribution $p(\Xb|\Xt)$, we use variational autoencoder to achieve this. In particular, our method is based on partial variational autoencoders (PVAE) which are designed to capture the underlying structure of features with missing values.

Peeking inside the Black Box: Interpreting Deep Learning Models for Exoplanet Atmospheric Retrievals

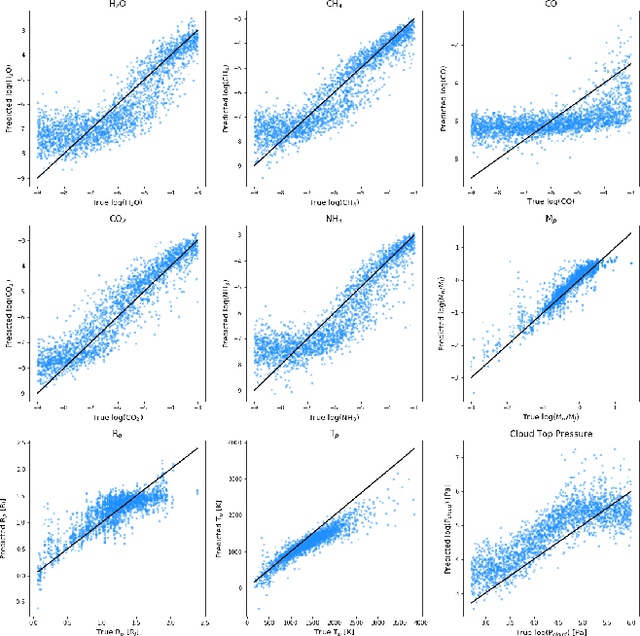
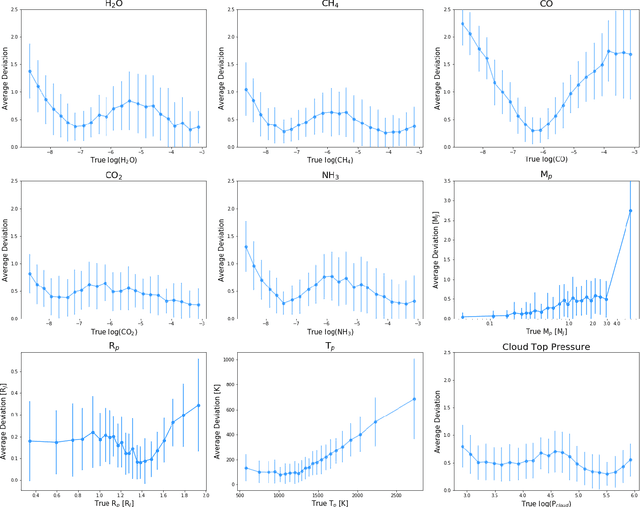
Deep learning algorithms are growing in popularity in the field of exoplanetary science due to their ability to model highly non-linear relations and solve interesting problems in a data-driven manner. Several works have attempted to perform fast retrievals of atmospheric parameters with the use of machine learning algorithms like deep neural networks (DNNs). Yet, despite their high predictive power, DNNs are also infamous for being 'black boxes'. It is their apparent lack of explainability that makes the astrophysics community reluctant to adopt them. What are their predictions based on? How confident should we be in them? When are they wrong and how wrong can they be? In this work, we present a number of general evaluation methodologies that can be applied to any trained model and answer questions like these. In particular, we train three different popular DNN architectures to retrieve atmospheric parameters from exoplanet spectra and show that all three achieve good predictive performance. We then present an extensive analysis of the predictions of DNNs, which can inform us - among other things - of the credibility limits for atmospheric parameters for a given instrument and model. Finally, we perform a perturbation-based sensitivity analysis to identify to which features of the spectrum the outcome of the retrieval is most sensitive. We conclude that for different molecules, the wavelength ranges to which the DNN's predictions are most sensitive, indeed coincide with their characteristic absorption regions. The methodologies presented in this work help to improve the evaluation of DNNs and to grant interpretability to their predictions.

Lessons Learned from the 1st ARIEL Machine Learning Challenge: Correcting Transiting Exoplanet Light Curves for Stellar Spots

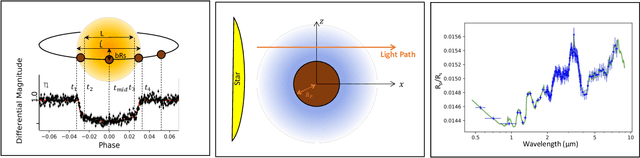
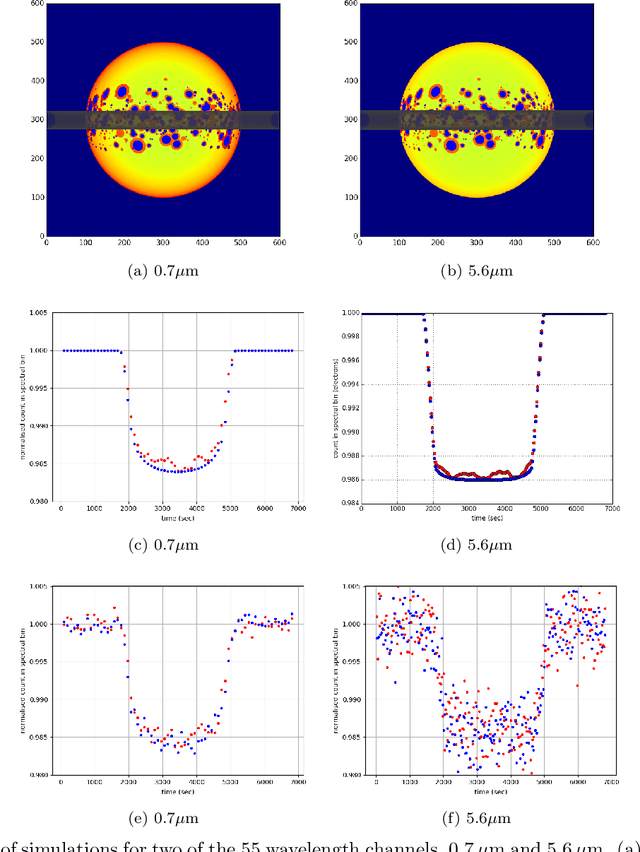
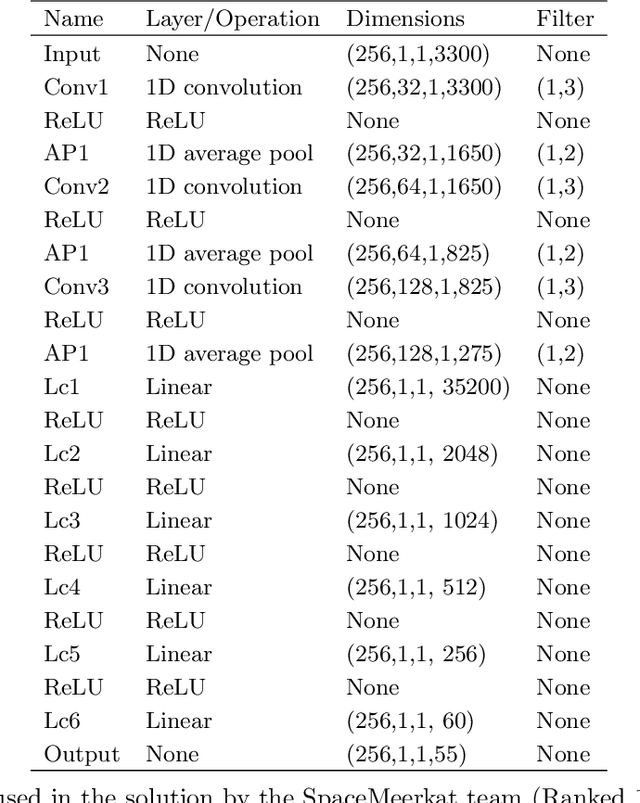
The last decade has witnessed a rapid growth of the field of exoplanet discovery and characterisation. However, several big challenges remain, many of which could be addressed using machine learning methodology. For instance, the most prolific method for detecting exoplanets and inferring several of their characteristics, transit photometry, is very sensitive to the presence of stellar spots. The current practice in the literature is to identify the effects of spots visually and correct for them manually or discard the affected data. This paper explores a first step towards fully automating the efficient and precise derivation of transit depths from transit light curves in the presence of stellar spots. The methods and results we present were obtained in the context of the 1st Machine Learning Challenge organized for the European Space Agency's upcoming Ariel mission. We first present the problem, the simulated Ariel-like data and outline the Challenge while identifying best practices for organizing similar challenges in the future. Finally, we present the solutions obtained by the top-5 winning teams, provide their code and discuss their implications. Successful solutions either construct highly non-linear (w.r.t. the raw data) models with minimal preprocessing -deep neural networks and ensemble methods- or amount to obtaining meaningful statistics from the light curves, constructing linear models on which yields comparably good predictive performance.