DiffSLT: Enhancing Diversity in Sign Language Translation via Diffusion Model

Sign language translation (SLT) is challenging, as it involves converting sign language videos into natural language. Previous studies have prioritized accuracy over diversity. However, diversity is crucial for handling lexical and syntactic ambiguities in machine translation, suggesting it could similarly benefit SLT. In this work, we propose DiffSLT, a novel gloss-free SLT framework that leverages a diffusion model, enabling diverse translations while preserving sign language semantics. DiffSLT transforms random noise into the target latent representation, conditioned on the visual features of input video. To enhance visual conditioning, we design Guidance Fusion Module, which fully utilizes the multi-level spatiotemporal information of the visual features. We also introduce DiffSLT-P, a DiffSLT variant that conditions on pseudo-glosses and visual features, providing key textual guidance and reducing the modality gap. As a result, DiffSLT and DiffSLT-P significantly improve diversity over previous gloss-free SLT methods and achieve state-of-the-art performance on two SLT datasets, thereby markedly improving translation quality.

Leveraging the Power of MLLMs for Gloss-Free Sign Language Translation

Sign language translation (SLT) is a challenging task that involves translating sign language images into spoken language. For SLT models to perform this task successfully, they must bridge the modality gap and identify subtle variations in sign language components to understand their meanings accurately. To address these challenges, we propose a novel gloss-free SLT framework called Multimodal Sign Language Translation (MMSLT), which leverages the representational capabilities of off-the-shelf multimodal large language models (MLLMs). Specifically, we generate detailed textual descriptions of sign language components using MLLMs. Then, through our proposed multimodal-language pre-training module, we integrate these description features with sign video features to align them within the spoken sentence space. Our approach achieves state-of-the-art performance on benchmark datasets PHOENIX14T and CSL-Daily, highlighting the potential of MLLMs to be effectively utilized in SLT.

Med-PerSAM: One-Shot Visual Prompt Tuning for Personalized Segment Anything Model in Medical Domain

Leveraging pre-trained models with tailored prompts for in-context learning has proven highly effective in NLP tasks. Building on this success, recent studies have applied a similar approach to the Segment Anything Model (SAM) within a ``one-shot" framework, where only a single reference image and its label are employed. However, these methods face limitations in the medical domain, primarily due to SAM's essential requirement for visual prompts and the over-reliance on pixel similarity for generating them. This dependency may lead to (1) inaccurate prompt generation and (2) clustering of point prompts, resulting in suboptimal outcomes. To address these challenges, we introduce \textbf{Med-PerSAM}, a novel and straightforward one-shot framework designed for the medical domain. Med-PerSAM uses only visual prompt engineering and eliminates the need for additional training of the pretrained SAM or human intervention, owing to our novel automated prompt generation process. By integrating our lightweight warping-based prompt tuning model with SAM, we enable the extraction and iterative refinement of visual prompts, enhancing the performance of the pre-trained SAM. This advancement is particularly meaningful in the medical domain, where creating visual prompts poses notable challenges for individuals lacking medical expertise. Our model outperforms various foundational models and previous SAM-based approaches across diverse 2D medical imaging datasets.

DPM: A Novel Training Method for Physics-Informed Neural Networks in Extrapolation

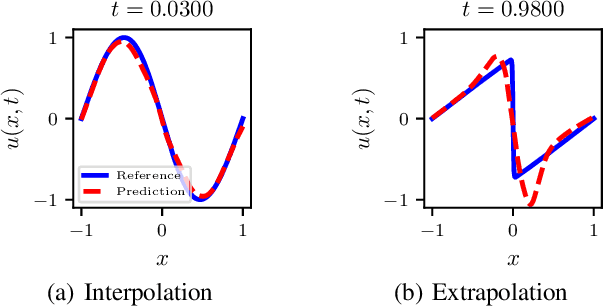
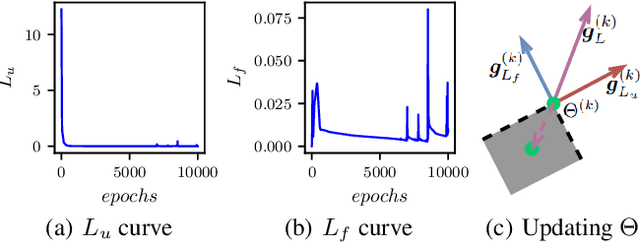
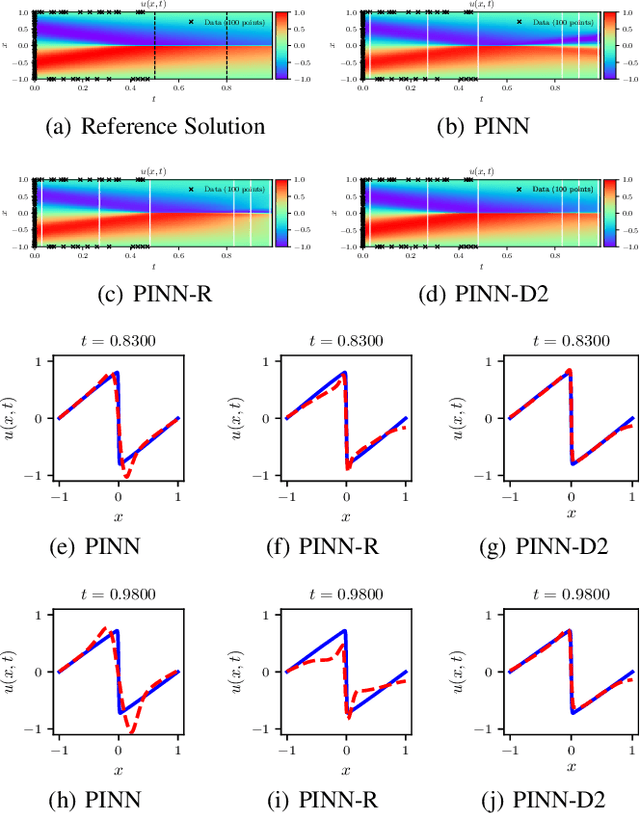
We present a method for learning dynamics of complex physical processes described by time-dependent nonlinear partial differential equations (PDEs). Our particular interest lies in extrapolating solutions in time beyond the range of temporal domain used in training. Our choice for a baseline method is physics-informed neural network (PINN) [Raissi et al., J. Comput. Phys., 378:686--707, 2019] because the method parameterizes not only the solutions but also the equations that describe the dynamics of physical processes. We demonstrate that PINN performs poorly on extrapolation tasks in many benchmark problems. To address this, we propose a novel method for better training PINN and demonstrate that our newly enhanced PINNs can accurately extrapolate solutions in time. Our method shows up to 72% smaller errors than existing methods in terms of the standard L2-norm metric.