A Novel Fast Exact Subproblem Solver for Stochastic Quasi-Newton Cubic Regularized Optimization

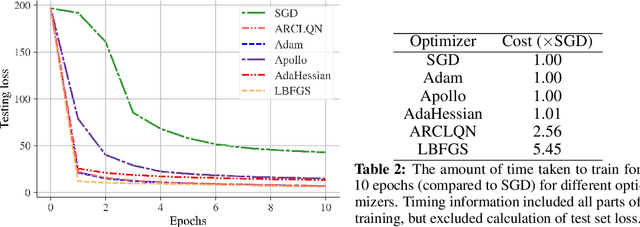
In this work we describe an Adaptive Regularization using Cubics (ARC) method for large-scale nonconvex unconstrained optimization using Limited-memory Quasi-Newton (LQN) matrices. ARC methods are a relatively new family of optimization strategies that utilize a cubic-regularization (CR) term in place of trust-regions and line-searches. LQN methods offer a large-scale alternative to using explicit second-order information by taking identical inputs to those used by popular first-order methods such as stochastic gradient descent (SGD). Solving the CR subproblem exactly requires Newton's method, yet using properties of the internal structure of LQN matrices, we are able to find exact solutions to the CR subproblem in a matrix-free manner, providing large speedups and scaling into modern size requirements. Additionally, we expand upon previous ARC work and explicitly incorporate first-order updates into our algorithm. We provide experimental results when the SR1 update is used, which show substantial speed-ups and competitive performance compared to Adam and other second order optimizers on deep neural networks (DNNs). We find that our new approach, ARCLQN, compares to modern optimizers with minimal tuning, a common pain-point for second order methods.

Constrained Multi-Objective Optimization for Automated Machine Learning

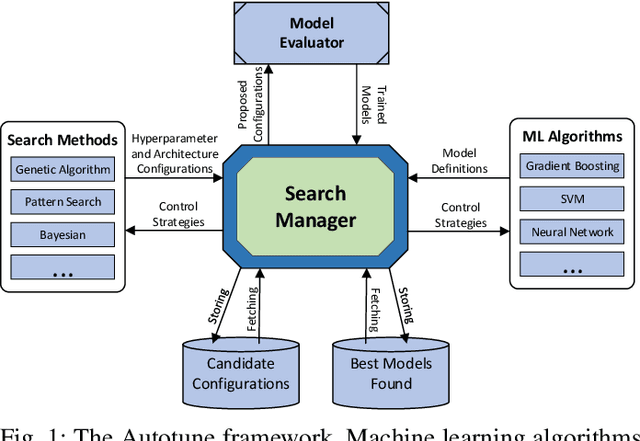
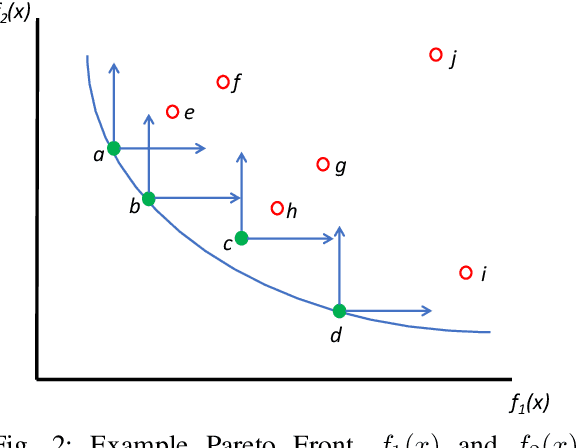
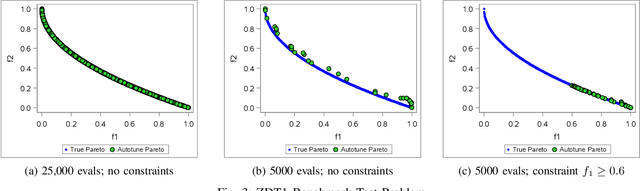
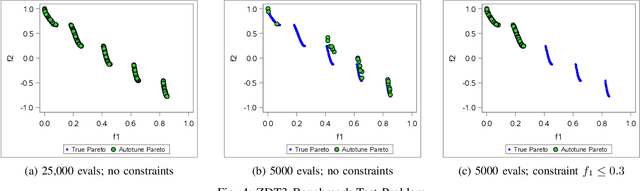
Automated machine learning has gained a lot of attention recently. Building and selecting the right machine learning models is often a multi-objective optimization problem. General purpose machine learning software that simultaneously supports multiple objectives and constraints is scant, though the potential benefits are great. In this work, we present a framework called Autotune that effectively handles multiple objectives and constraints that arise in machine learning problems. Autotune is built on a suite of derivative-free optimization methods, and utilizes multi-level parallelism in a distributed computing environment for automatically training, scoring, and selecting good models. Incorporation of multiple objectives and constraints in the model exploration and selection process provides the flexibility needed to satisfy trade-offs necessary in practical machine learning applications. Experimental results from standard multi-objective optimization benchmark problems show that Autotune is very efficient in capturing Pareto fronts. These benchmark results also show how adding constraints can guide the search to more promising regions of the solution space, ultimately producing more desirable Pareto fronts. Results from two real-world case studies demonstrate the effectiveness of the constrained multi-objective optimization capability offered by Autotune.

High-Performance Support Vector Machines and Its Applications

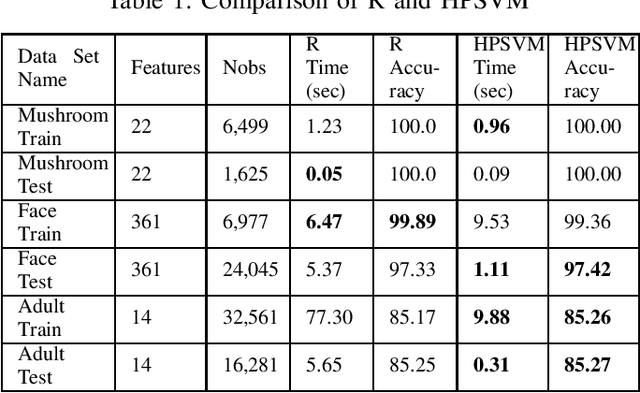
The support vector machines (SVM) algorithm is a popular classification technique in data mining and machine learning. In this paper, we propose a distributed SVM algorithm and demonstrate its use in a number of applications. The algorithm is named high-performance support vector machines (HPSVM). The major contribution of HPSVM is two-fold. First, HPSVM provides a new way to distribute computations to the machines in the cloud without shuffling the data. Second, HPSVM minimizes the inter-machine communications in order to maximize the performance. We apply HPSVM to some real-world classification problems and compare it with the state-of-the-art SVM technique implemented in R on several public data sets. HPSVM achieves similar or better results.

Autotune: A Derivative-free Optimization Framework for Hyperparameter Tuning

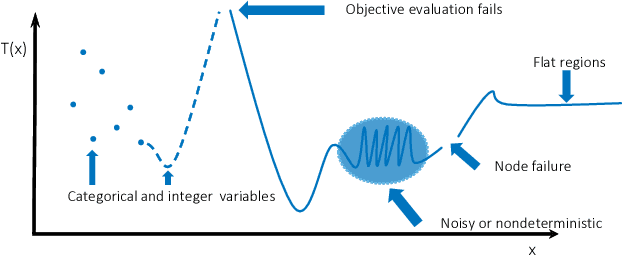
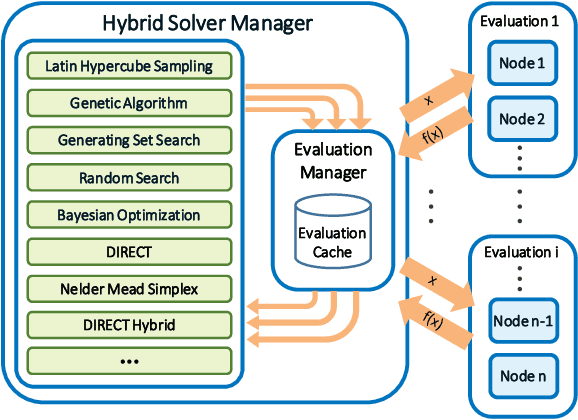
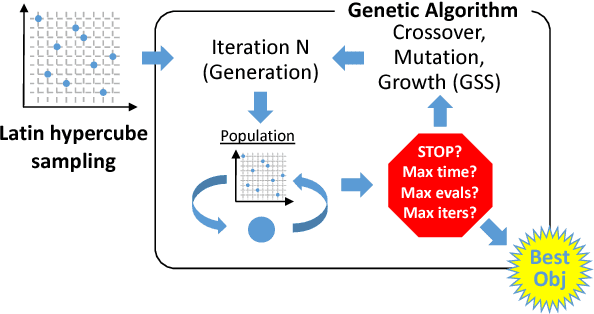
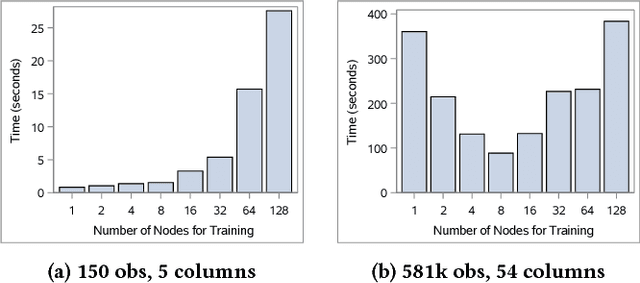
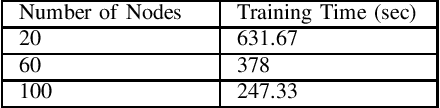
Machine learning applications often require hyperparameter tuning. The hyperparameters usually drive both the efficiency of the model training process and the resulting model quality. For hyperparameter tuning, machine learning algorithms are complex black-boxes. This creates a class of challenging optimization problems, whose objective functions tend to be nonsmooth, discontinuous, unpredictably varying in computational expense, and include continuous, categorical, and/or integer variables. Further, function evaluations can fail for a variety of reasons including numerical difficulties or hardware failures. Additionally, not all hyperparameter value combinations are compatible, which creates so called hidden constraints. Robust and efficient optimization algorithms are needed for hyperparameter tuning. In this paper we present an automated parallel derivative-free optimization framework called \textbf{Autotune}, which combines a number of specialized sampling and search methods that are very effective in tuning machine learning models despite these challenges. Autotune provides significantly improved models over using default hyperparameter settings with minimal user interaction on real-world applications. Given the inherent expense of training numerous candidate models, we demonstrate the effectiveness of Autotune's search methods and the efficient distributed and parallel paradigms for training and tuning models, and also discuss the resource trade-offs associated with the ability to both distribute the training process and parallelize the tuning process.

Trust-Region Algorithms for Training Responses: Machine Learning Methods Using Indefinite Hessian Approximations

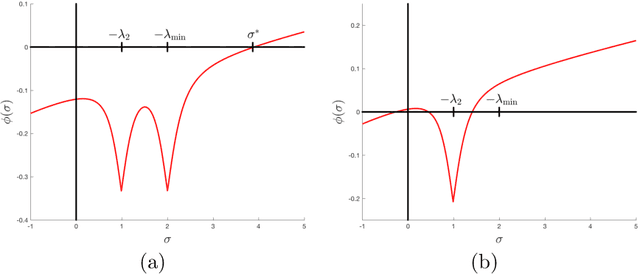
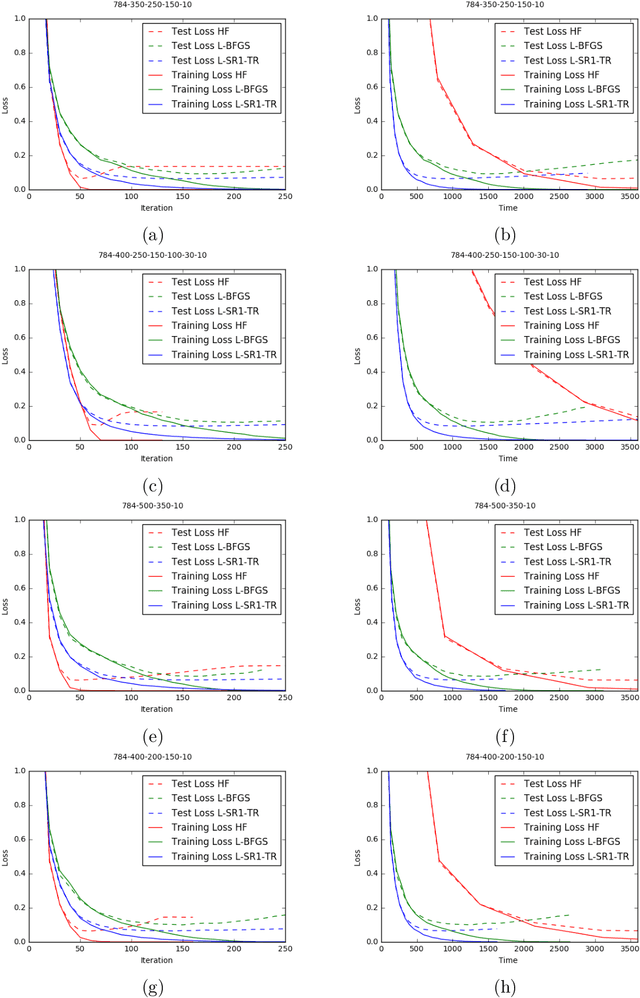
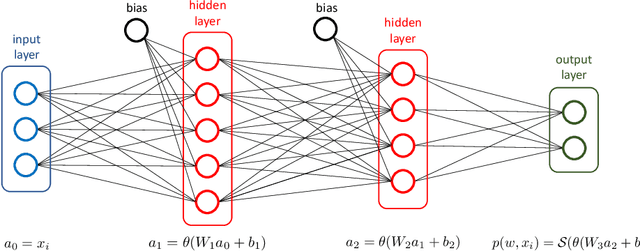
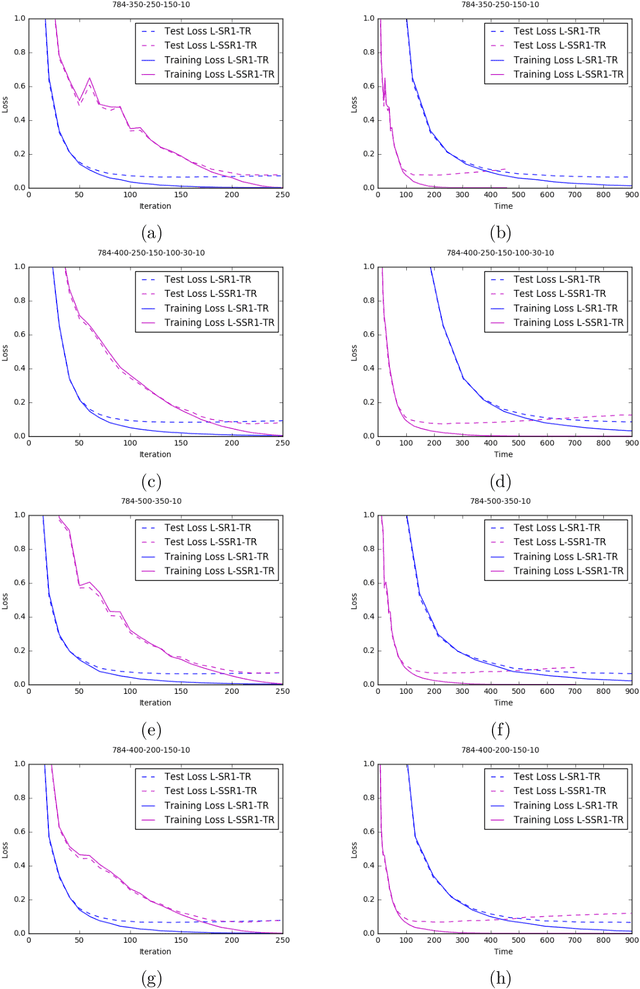
Machine learning (ML) problems are often posed as highly nonlinear and nonconvex unconstrained optimization problems. Methods for solving ML problems based on stochastic gradient descent are easily scaled for very large problems but may involve fine-tuning many hyper-parameters. Quasi-Newton approaches based on the limited-memory Broyden-Fletcher-Goldfarb-Shanno (BFGS) update typically do not require manually tuning hyper-parameters but suffer from approximating a potentially indefinite Hessian with a positive-definite matrix. Hessian-free methods leverage the ability to perform Hessian-vector multiplication without needing the entire Hessian matrix, but each iteration's complexity is significantly greater than quasi-Newton methods. In this paper we propose an alternative approach for solving ML problems based on a quasi-Newton trust-region framework for solving large-scale optimization problems that allow for indefinite Hessian approximations. Numerical experiments on a standard testing data set show that with a fixed computational time budget, the proposed methods achieve better results than the traditional limited-memory BFGS and the Hessian-free methods.