A Block Metropolis-Hastings Sampler for Controllable Energy-based Text Generation

Recent work has shown that energy-based language modeling is an effective framework for controllable text generation because it enables flexible integration of arbitrary discriminators. However, because energy-based LMs are globally normalized, approximate techniques like Metropolis-Hastings (MH) are required for inference. Past work has largely explored simple proposal distributions that modify a single token at a time, like in Gibbs sampling. In this paper, we develop a novel MH sampler that, in contrast, proposes re-writes of the entire sequence in each step via iterative prompting of a large language model. Our new sampler (a) allows for more efficient and accurate sampling from a target distribution and (b) allows generation length to be determined through the sampling procedure rather than fixed in advance, as past work has required. We perform experiments on two controlled generation tasks, showing both downstream performance gains and more accurate target distribution sampling in comparison with single-token proposal techniques.

Assessing Out-of-Domain Language Model Performance from Few Examples

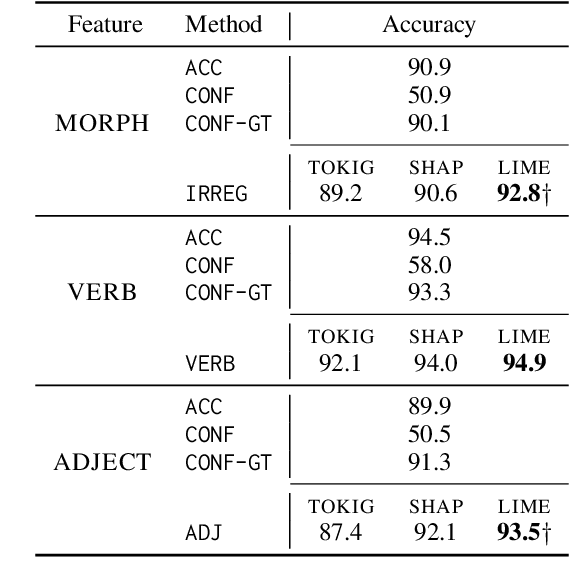
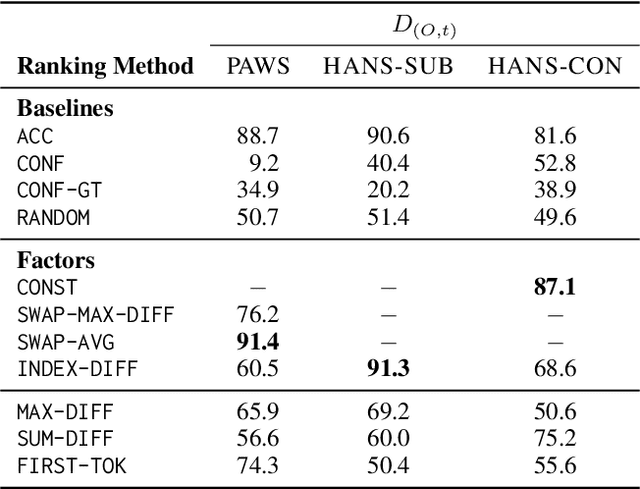
While pretrained language models have exhibited impressive generalization capabilities, they still behave unpredictably under certain domain shifts. In particular, a model may learn a reasoning process on in-domain training data that does not hold for out-of-domain test data. We address the task of predicting out-of-domain (OOD) performance in a few-shot fashion: given a few target-domain examples and a set of models with similar training performance, can we understand how these models will perform on OOD test data? We benchmark the performance on this task when looking at model accuracy on the few-shot examples, then investigate how to incorporate analysis of the models' behavior using feature attributions to better tackle this problem. Specifically, we explore a set of "factors" designed to reveal model agreement with certain pathological heuristics that may indicate worse generalization capabilities. On textual entailment, paraphrase recognition, and a synthetic classification task, we show that attribution-based factors can help rank relative model OOD performance. However, accuracy on a few-shot test set is a surprisingly strong baseline, particularly when the system designer does not have in-depth prior knowledge about the domain shift.

A Novel Fast Exact Subproblem Solver for Stochastic Quasi-Newton Cubic Regularized Optimization

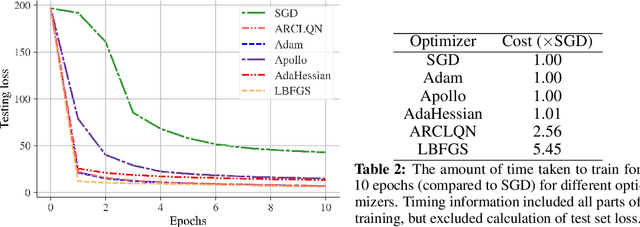
In this work we describe an Adaptive Regularization using Cubics (ARC) method for large-scale nonconvex unconstrained optimization using Limited-memory Quasi-Newton (LQN) matrices. ARC methods are a relatively new family of optimization strategies that utilize a cubic-regularization (CR) term in place of trust-regions and line-searches. LQN methods offer a large-scale alternative to using explicit second-order information by taking identical inputs to those used by popular first-order methods such as stochastic gradient descent (SGD). Solving the CR subproblem exactly requires Newton's method, yet using properties of the internal structure of LQN matrices, we are able to find exact solutions to the CR subproblem in a matrix-free manner, providing large speedups and scaling into modern size requirements. Additionally, we expand upon previous ARC work and explicitly incorporate first-order updates into our algorithm. We provide experimental results when the SR1 update is used, which show substantial speed-ups and competitive performance compared to Adam and other second order optimizers on deep neural networks (DNNs). We find that our new approach, ARCLQN, compares to modern optimizers with minimal tuning, a common pain-point for second order methods.