Sparse Signal Reconstruction for Overdispersed Low-photon Count Biomedical Imaging Using $\ell_p$ Total Variation

The negative binomial model, which generalizes the Poisson distribution model, can be found in applications involving low-photon signal recovery, including medical imaging. Recent studies have explored several regularization terms for the negative binomial model, such as the $\ell_p$ quasi-norm with $0 < p < 1$, $\ell_1$ norm, and the total variation (TV) quasi-seminorm for promoting sparsity in signal recovery. These penalty terms have been shown to improve image reconstruction outcomes. In this paper, we investigate the $\ell_p$ quasi-seminorm, both isotropic and anisotropic $\ell_p$ TV quasi-seminorms, within the framework of the negative binomial statistical model. This problem can be formulated as an optimization problem, which we solve using a gradient-based approach. We present comparisons between the negative binomial and Poisson statistical models using the $\ell_p$ TV quasi-seminorm as well as common penalty terms. Our experimental results highlight the efficacy of the proposed method.

Negative Binomial Matrix Completion

Matrix completion focuses on recovering missing or incomplete information in matrices. This problem arises in various applications, including image processing and network analysis. Previous research proposed Poisson matrix completion for count data with noise that follows a Poisson distribution, which assumes that the mean and variance are equal. Since overdispersed count data, whose variance is greater than the mean, is more likely to occur in realistic settings, we assume that the noise follows the negative binomial (NB) distribution, which can be more general than the Poisson distribution. In this paper, we introduce NB matrix completion by proposing a nuclear-norm regularized model that can be solved by proximal gradient descent. In our experiments, we demonstrate that the NB model outperforms Poisson matrix completion in various noise and missing data settings on real data.

Quasi-Newton Optimization Methods For Deep Learning Applications

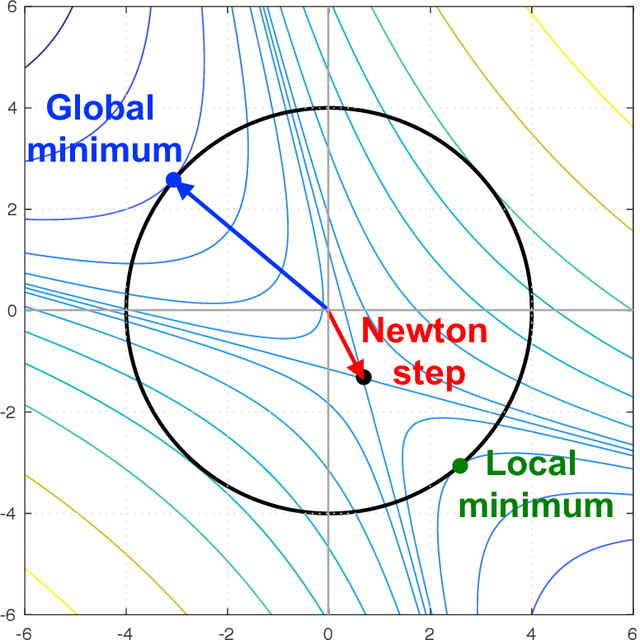
Deep learning algorithms often require solving a highly non-linear and nonconvex unconstrained optimization problem. Methods for solving optimization problems in large-scale machine learning, such as deep learning and deep reinforcement learning (RL), are generally restricted to the class of first-order algorithms, like stochastic gradient descent (SGD). While SGD iterates are inexpensive to compute, they have slow theoretical convergence rates. Furthermore, they require exhaustive trial-and-error to fine-tune many learning parameters. Using second-order curvature information to find search directions can help with more robust convergence for non-convex optimization problems. However, computing Hessian matrices for large-scale problems is not computationally practical. Alternatively, quasi-Newton methods construct an approximate of the Hessian matrix to build a quadratic model of the objective function. Quasi-Newton methods, like SGD, require only first-order gradient information, but they can result in superlinear convergence, which makes them attractive alternatives to SGD. The limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) approach is one of the most popular quasi-Newton methods that construct positive definite Hessian approximations. In this chapter, we propose efficient optimization methods based on L-BFGS quasi-Newton methods using line search and trust-region strategies. Our methods bridge the disparity between first- and second-order methods by using gradient information to calculate low-rank updates to Hessian approximations. We provide formal convergence analysis of these methods as well as empirical results on deep learning applications, such as image classification tasks and deep reinforcement learning on a set of ATARI 2600 video games. Our results show a robust convergence with preferred generalization characteristics as well as fast training time.

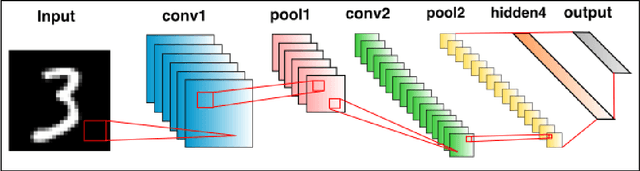
Quasi-Newton Optimization in Deep Q-Learning for Playing ATARI Games

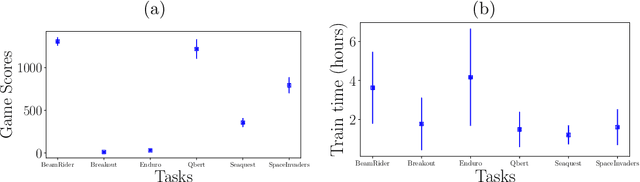
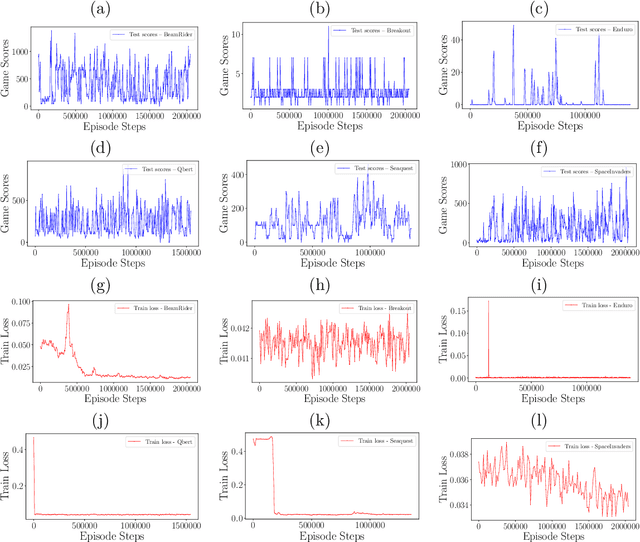
Reinforcement Learning (RL) algorithms allow artificial agents to improve their selection of actions so as to increase rewarding experiences in their environments. The learning can become intractably slow as the state space of the environment grows. This has motivated methods to use deep artificial neural networks to learn the state representations. Deep reinforcement learning algorithms require solving a non-convex and nonlinear unconstrained optimization problem. Methods for solving the optimization problems in deep RL are restricted to the class of first-order algorithms, like stochastic gradient descent (SGD). The major drawback of the SGD methods is that they have the undesirable effect of not escaping saddle points. Furthermore, these methods require exhaustive trial and error to fine-tune many learning parameters. Using second derivative information can result in improved convergence properties, but computing the Hessian matrix for large-scale problems is not practical. Quasi-Newton methods, like SGD, require only first-order gradient information, but they can result in superlinear convergence, which makes them attractive alternatives. The limited-memory BFGS approach is one of the most popular quasi-Newton methods that construct positive definite Hessian approximations. In this paper, we introduce an efficient optimization method, based on the limited memory BFGS quasi-Newton method using line search strategy -- as an alternative to SGD methods. Our method bridges the disparity between first order methods and second order methods by continuing to use gradient information to calculate a low-rank Hessian approximations. We provide empirical results on variety of the classic ATARI 2600 games. Our results show a robust convergence with preferred generalization characteristics, as well as fast training time and no need for the experience replaying mechanism.

Trust-Region Algorithms for Training Responses: Machine Learning Methods Using Indefinite Hessian Approximations

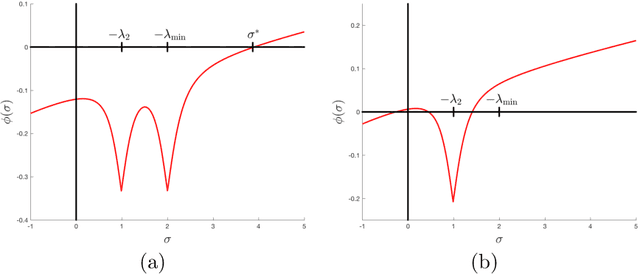
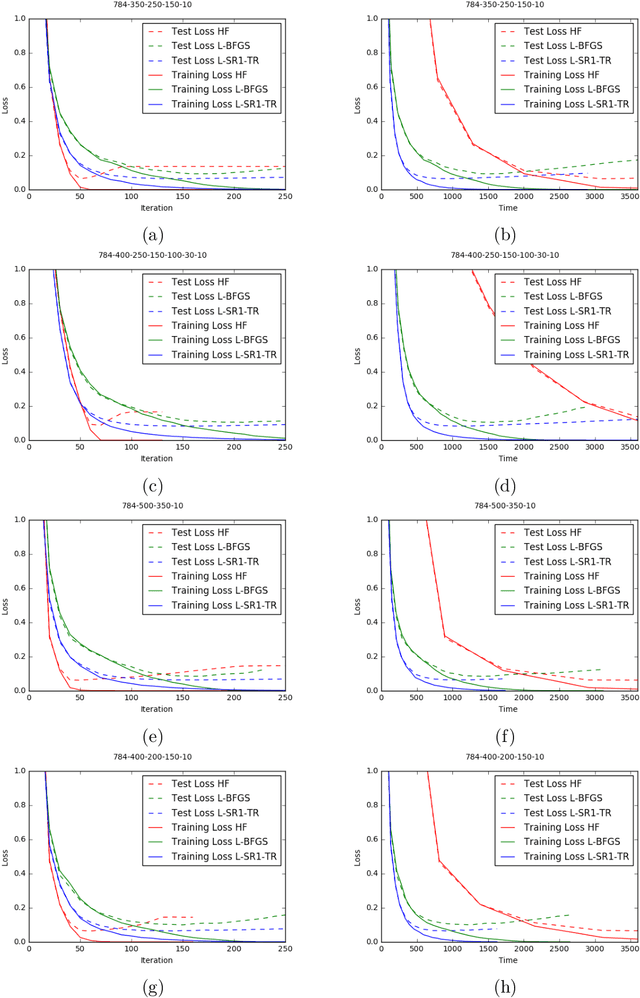
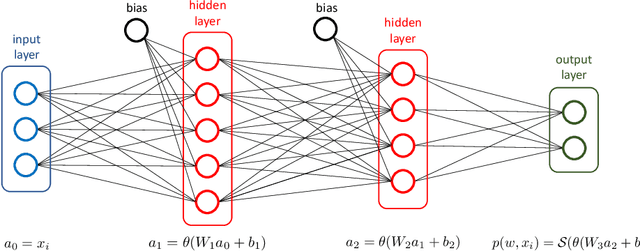
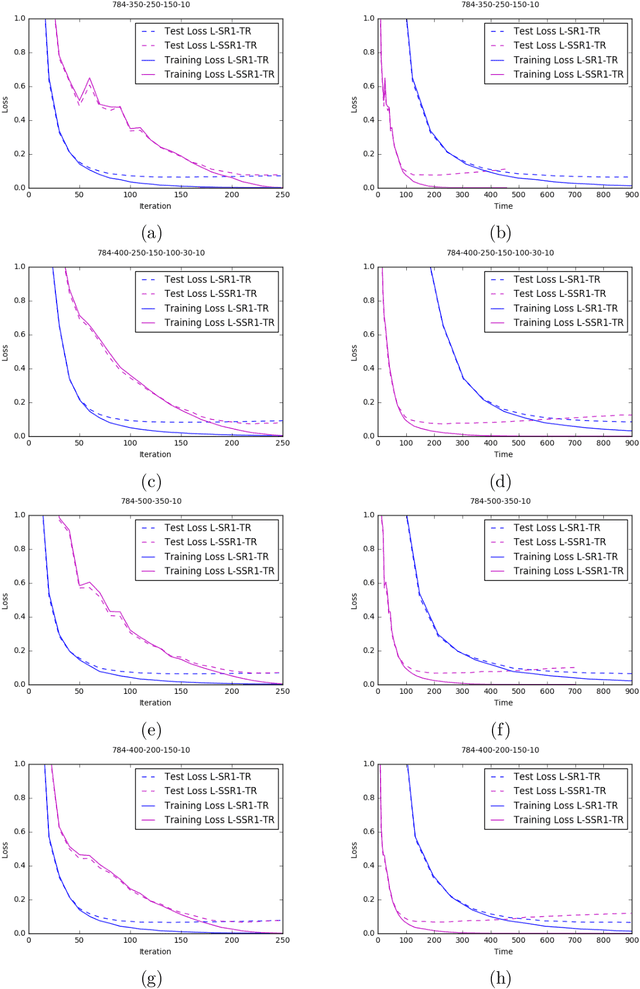
Machine learning (ML) problems are often posed as highly nonlinear and nonconvex unconstrained optimization problems. Methods for solving ML problems based on stochastic gradient descent are easily scaled for very large problems but may involve fine-tuning many hyper-parameters. Quasi-Newton approaches based on the limited-memory Broyden-Fletcher-Goldfarb-Shanno (BFGS) update typically do not require manually tuning hyper-parameters but suffer from approximating a potentially indefinite Hessian with a positive-definite matrix. Hessian-free methods leverage the ability to perform Hessian-vector multiplication without needing the entire Hessian matrix, but each iteration's complexity is significantly greater than quasi-Newton methods. In this paper we propose an alternative approach for solving ML problems based on a quasi-Newton trust-region framework for solving large-scale optimization problems that allow for indefinite Hessian approximations. Numerical experiments on a standard testing data set show that with a fixed computational time budget, the proposed methods achieve better results than the traditional limited-memory BFGS and the Hessian-free methods.

Compressive Coded Aperture Keyed Exposure Imaging with Optical Flow Reconstruction

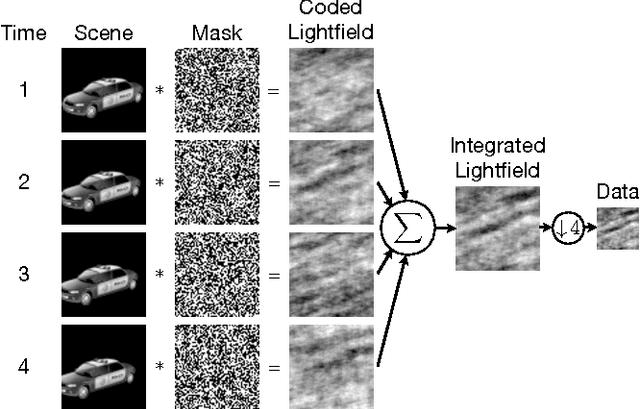
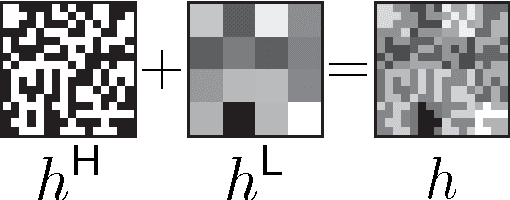
This paper describes a coded aperture and keyed exposure approach to compressive video measurement which admits a small physical platform, high photon efficiency, high temporal resolution, and fast reconstruction algorithms. The proposed projections satisfy the Restricted Isometry Property (RIP), and hence compressed sensing theory provides theoretical guarantees on the video reconstruction quality. Moreover, the projections can be easily implemented using existing optical elements such as spatial light modulators (SLMs). We extend these coded mask designs to novel dual-scale masks (DSMs) which enable the recovery of a coarse-resolution estimate of the scene with negligible computational cost. We develop fast numerical algorithms which utilize both temporal correlations and optical flow in the video sequence as well as the innovative structure of the projections. Our numerical experiments demonstrate the efficacy of the proposed approach on short-wave infrared data.