Quasi-Newton Optimization in Deep Q-Learning for Playing ATARI Games

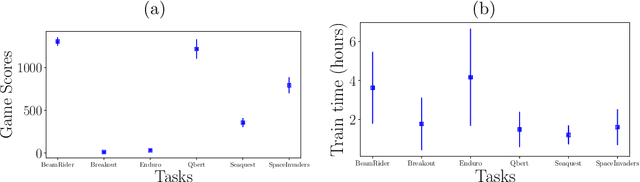
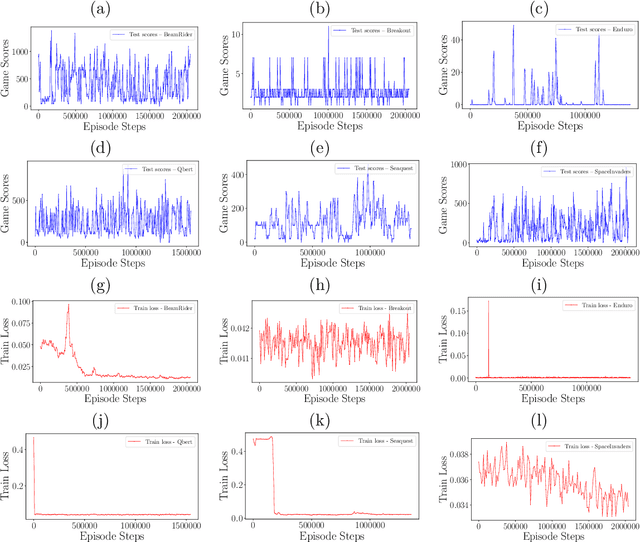
Reinforcement Learning (RL) algorithms allow artificial agents to improve their selection of actions so as to increase rewarding experiences in their environments. The learning can become intractably slow as the state space of the environment grows. This has motivated methods to use deep artificial neural networks to learn the state representations. Deep reinforcement learning algorithms require solving a non-convex and nonlinear unconstrained optimization problem. Methods for solving the optimization problems in deep RL are restricted to the class of first-order algorithms, like stochastic gradient descent (SGD). The major drawback of the SGD methods is that they have the undesirable effect of not escaping saddle points. Furthermore, these methods require exhaustive trial and error to fine-tune many learning parameters. Using second derivative information can result in improved convergence properties, but computing the Hessian matrix for large-scale problems is not practical. Quasi-Newton methods, like SGD, require only first-order gradient information, but they can result in superlinear convergence, which makes them attractive alternatives. The limited-memory BFGS approach is one of the most popular quasi-Newton methods that construct positive definite Hessian approximations. In this paper, we introduce an efficient optimization method, based on the limited memory BFGS quasi-Newton method using line search strategy -- as an alternative to SGD methods. Our method bridges the disparity between first order methods and second order methods by continuing to use gradient information to calculate a low-rank Hessian approximations. We provide empirical results on variety of the classic ATARI 2600 games. Our results show a robust convergence with preferred generalization characteristics, as well as fast training time and no need for the experience replaying mechanism.