Efficient Exploration through Intrinsic Motivation Learning for Unsupervised Subgoal Discovery in Model-Free Hierarchical Reinforcement Learning

Efficient exploration for automatic subgoal discovery is a challenging problem in Hierarchical Reinforcement Learning (HRL). In this paper, we show that intrinsic motivation learning increases the efficiency of exploration, leading to successful subgoal discovery. We introduce a model-free subgoal discovery method based on unsupervised learning over a limited memory of agent's experiences during intrinsic motivation. Additionally, we offer a unified approach to learning representations in model-free HRL.

Quasi-Newton Optimization Methods For Deep Learning Applications

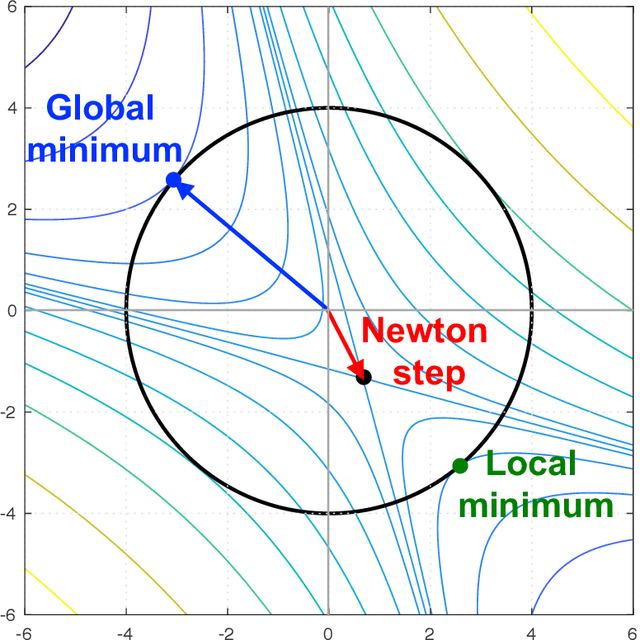
Deep learning algorithms often require solving a highly non-linear and nonconvex unconstrained optimization problem. Methods for solving optimization problems in large-scale machine learning, such as deep learning and deep reinforcement learning (RL), are generally restricted to the class of first-order algorithms, like stochastic gradient descent (SGD). While SGD iterates are inexpensive to compute, they have slow theoretical convergence rates. Furthermore, they require exhaustive trial-and-error to fine-tune many learning parameters. Using second-order curvature information to find search directions can help with more robust convergence for non-convex optimization problems. However, computing Hessian matrices for large-scale problems is not computationally practical. Alternatively, quasi-Newton methods construct an approximate of the Hessian matrix to build a quadratic model of the objective function. Quasi-Newton methods, like SGD, require only first-order gradient information, but they can result in superlinear convergence, which makes them attractive alternatives to SGD. The limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) approach is one of the most popular quasi-Newton methods that construct positive definite Hessian approximations. In this chapter, we propose efficient optimization methods based on L-BFGS quasi-Newton methods using line search and trust-region strategies. Our methods bridge the disparity between first- and second-order methods by using gradient information to calculate low-rank updates to Hessian approximations. We provide formal convergence analysis of these methods as well as empirical results on deep learning applications, such as image classification tasks and deep reinforcement learning on a set of ATARI 2600 video games. Our results show a robust convergence with preferred generalization characteristics as well as fast training time.

Learning sparse representations in reinforcement learning

Reinforcement learning (RL) algorithms allow artificial agents to improve their selection of actions to increase rewarding experiences in their environments. Temporal Difference (TD) Learning -- a model-free RL method -- is a leading account of the midbrain dopamine system and the basal ganglia in reinforcement learning. These algorithms typically learn a mapping from the agent's current sensed state to a selected action (known as a policy function) via learning a value function (expected future rewards). TD Learning methods have been very successful on a broad range of control tasks, but learning can become intractably slow as the state space of the environment grows. This has motivated methods that learn internal representations of the agent's state, effectively reducing the size of the state space and restructuring state representations in order to support generalization. However, TD Learning coupled with an artificial neural network, as a function approximator, has been shown to fail to learn some fairly simple control tasks, challenging this explanation of reward-based learning. We hypothesize that such failures do not arise in the brain because of the ubiquitous presence of lateral inhibition in the cortex, producing sparse distributed internal representations that support the learning of expected future reward. The sparse conjunctive representations can avoid catastrophic interference while still supporting generalization. We provide support for this conjecture through computational simulations, demonstrating the benefits of learned sparse representations for three problematic classic control tasks: Puddle-world, Mountain-car, and Acrobot.

Quasi-Newton Optimization in Deep Q-Learning for Playing ATARI Games

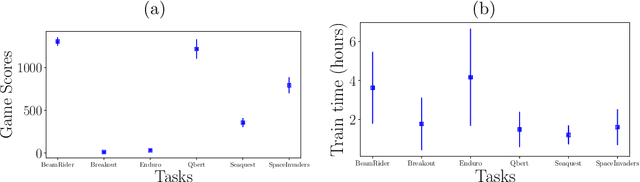
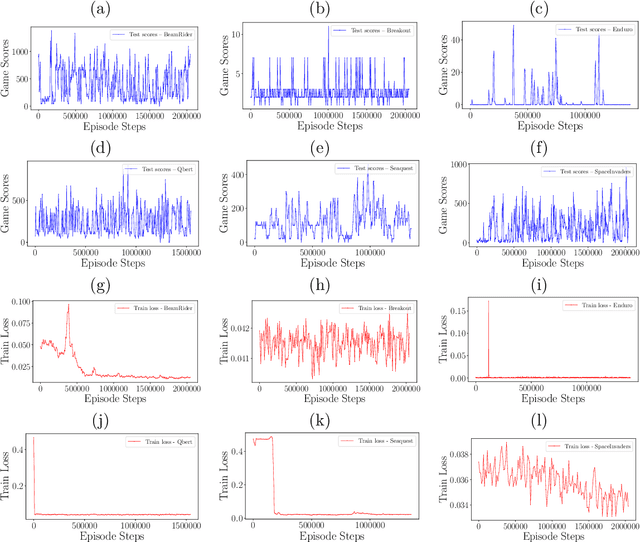
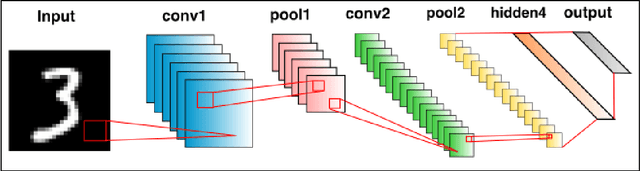
Reinforcement Learning (RL) algorithms allow artificial agents to improve their selection of actions so as to increase rewarding experiences in their environments. The learning can become intractably slow as the state space of the environment grows. This has motivated methods to use deep artificial neural networks to learn the state representations. Deep reinforcement learning algorithms require solving a non-convex and nonlinear unconstrained optimization problem. Methods for solving the optimization problems in deep RL are restricted to the class of first-order algorithms, like stochastic gradient descent (SGD). The major drawback of the SGD methods is that they have the undesirable effect of not escaping saddle points. Furthermore, these methods require exhaustive trial and error to fine-tune many learning parameters. Using second derivative information can result in improved convergence properties, but computing the Hessian matrix for large-scale problems is not practical. Quasi-Newton methods, like SGD, require only first-order gradient information, but they can result in superlinear convergence, which makes them attractive alternatives. The limited-memory BFGS approach is one of the most popular quasi-Newton methods that construct positive definite Hessian approximations. In this paper, we introduce an efficient optimization method, based on the limited memory BFGS quasi-Newton method using line search strategy -- as an alternative to SGD methods. Our method bridges the disparity between first order methods and second order methods by continuing to use gradient information to calculate a low-rank Hessian approximations. We provide empirical results on variety of the classic ATARI 2600 games. Our results show a robust convergence with preferred generalization characteristics, as well as fast training time and no need for the experience replaying mechanism.

Learning Representations in Model-Free Hierarchical Reinforcement Learning

Common approaches to Reinforcement Learning (RL) are seriously challenged by large-scale applications involving huge state spaces and sparse delayed reward feedback. Hierarchical Reinforcement Learning (HRL) methods attempt to address this scalability issue by learning action selection policies at multiple levels of temporal abstraction. Abstraction can be had by identifying a relatively small set of states that are likely to be useful as subgoals, in concert with the learning of corresponding skill policies to achieve those subgoals. Many approaches to subgoal discovery in HRL depend on the analysis of a model of the environment, but the need to learn such a model introduces its own problems of scale. Once subgoals are identified, skills may be learned through intrinsic motivation, introducing an internal reward signal marking subgoal attainment. In this paper, we present a novel model-free method for subgoal discovery using incremental unsupervised learning over a small memory of the most recent experiences of the agent. When combined with an intrinsic motivation learning mechanism, this method learns subgoals and skills together, based on experiences in the environment. Thus, we offer an original approach to HRL that does not require the acquisition of a model of the environment, suitable for large-scale applications. We demonstrate the efficiency of our method on two RL problems with sparse delayed feedback: a variant of the rooms environment and the ATARI 2600 game called Montezuma's Revenge.