Tracking Dynamic Point Processes on Networks

Cascading chains of events are a salient feature of many real-world social, biological, and financial networks. In social networks, social reciprocity accounts for retaliations in gang interactions, proxy wars in nation-state conflicts, or Internet memes shared via social media. Neuron spikes stimulate or inhibit spike activity in other neurons. Stock market shocks can trigger a contagion of volatility throughout a financial network. In these and other examples, only individual events associated with network nodes are observed, usually without knowledge of the underlying dynamic relationships between nodes. This paper addresses the challenge of tracking how events within such networks stimulate or influence future events. The proposed approach is an online learning framework well-suited to streaming data, using a multivariate Hawkes point process model to encapsulate autoregressive features of observed events within the social network. Recent work on online learning in dynamic environments is leveraged not only to exploit the dynamics within the underlying network, but also to track the network structure as it evolves. Regret bounds and experimental results demonstrate that the proposed method performs nearly as well as an oracle or batch algorithm.

Online Optimization in Dynamic Environments

High-velocity streams of high-dimensional data pose significant "big data" analysis challenges across a range of applications and settings. Online learning and online convex programming play a significant role in the rapid recovery of important or anomalous information from these large datastreams. While recent advances in online learning have led to novel and rapidly converging algorithms, these methods are unable to adapt to nonstationary environments arising in real-world problems. This paper describes a dynamic mirror descent framework which addresses this challenge, yielding low theoretical regret bounds and accurate, adaptive, and computationally efficient algorithms which are applicable to broad classes of problems. The methods are capable of learning and adapting to an underlying and possibly time-varying dynamical model. Empirical results in the context of dynamic texture analysis, solar flare detection, sequential compressed sensing of a dynamic scene, traffic surveillance,tracking self-exciting point processes and network behavior in the Enron email corpus support the core theoretical findings.

Learning Single Index Models in High Dimensions

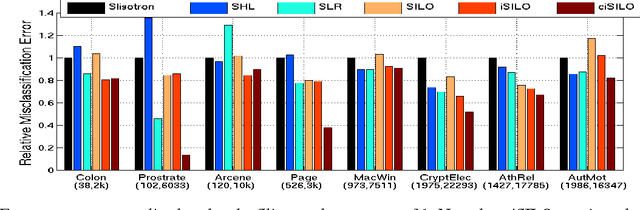
Single Index Models (SIMs) are simple yet flexible semi-parametric models for classification and regression. Response variables are modeled as a nonlinear, monotonic function of a linear combination of features. Estimation in this context requires learning both the feature weights, and the nonlinear function. While methods have been described to learn SIMs in the low dimensional regime, a method that can efficiently learn SIMs in high dimensions has not been forthcoming. We propose three variants of a computationally and statistically efficient algorithm for SIM inference in high dimensions. We establish excess risk bounds for the proposed algorithms and experimentally validate the advantages that our SIM learning methods provide relative to Generalized Linear Model (GLM) and low dimensional SIM based learning methods.

Sparse Linear Regression With Missing Data

This paper proposes a fast and accurate method for sparse regression in the presence of missing data. The underlying statistical model encapsulates the low-dimensional structure of the incomplete data matrix and the sparsity of the regression coefficients, and the proposed algorithm jointly learns the low-dimensional structure of the data and a linear regressor with sparse coefficients. The proposed stochastic optimization method, Sparse Linear Regression with Missing Data (SLRM), performs an alternating minimization procedure and scales well with the problem size. Large deviation inequalities shed light on the impact of the various problem-dependent parameters on the expected squared loss of the learned regressor. Extensive simulations on both synthetic and real datasets show that SLRM performs better than competing algorithms in a variety of contexts.

Compressive Coded Aperture Keyed Exposure Imaging with Optical Flow Reconstruction

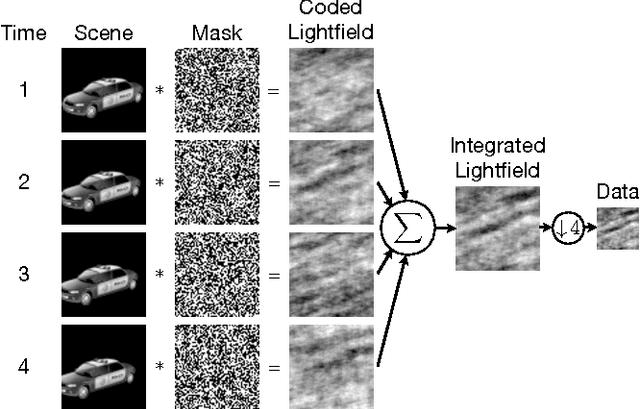
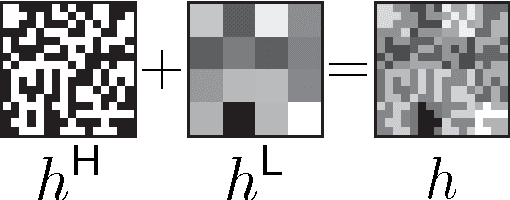
This paper describes a coded aperture and keyed exposure approach to compressive video measurement which admits a small physical platform, high photon efficiency, high temporal resolution, and fast reconstruction algorithms. The proposed projections satisfy the Restricted Isometry Property (RIP), and hence compressed sensing theory provides theoretical guarantees on the video reconstruction quality. Moreover, the projections can be easily implemented using existing optical elements such as spatial light modulators (SLMs). We extend these coded mask designs to novel dual-scale masks (DSMs) which enable the recovery of a coarse-resolution estimate of the scene with negligible computational cost. We develop fast numerical algorithms which utilize both temporal correlations and optical flow in the video sequence as well as the innovative structure of the projections. Our numerical experiments demonstrate the efficacy of the proposed approach on short-wave infrared data.

Dynamical Models and Tracking Regret in Online Convex Programming

This paper describes a new online convex optimization method which incorporates a family of candidate dynamical models and establishes novel tracking regret bounds that scale with the comparator's deviation from the best dynamical model in this family. Previous online optimization methods are designed to have a total accumulated loss comparable to that of the best comparator sequence, and existing tracking or shifting regret bounds scale with the overall variation of the comparator sequence. In many practical scenarios, however, the environment is nonstationary and comparator sequences with small variation are quite weak, resulting in large losses. The proposed Dynamic Mirror Descent method, in contrast, can yield low regret relative to highly variable comparator sequences by both tracking the best dynamical model and forming predictions based on that model. This concept is demonstrated empirically in the context of sequential compressive observations of a dynamic scene and tracking a dynamic social network.