Change Point Detection With Conceptors

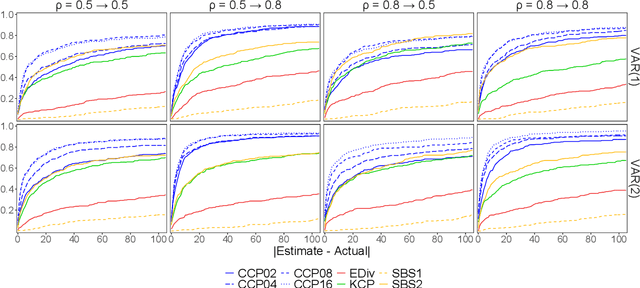
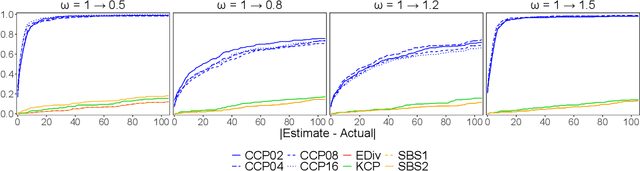
Offline change point detection seeks to identify points in a time series where the data generating process changes. This problem is well studied for univariate i.i.d. data, but becomes challenging with increasing dimension and temporal dependence. For the at most one change point problem, we propose the use of a conceptor matrix to learn the characteristic dynamics of a specified training window in a time series. The associated random recurrent neural network acts as a featurizer of the data, and change points are identified from a univariate quantification of the distance between the featurization and the space spanned by a representative conceptor matrix. This model agnostic method can suggest potential locations of interest that warrant further study. We prove that, under mild assumptions, the method provides a consistent estimate of the true change point, and quantile estimates for statistics are produced via a moving block bootstrap of the original data. The method is tested on simulations from several classes of processes, and we evaluate performance with clustering metrics, graphical methods, and observed Type 1 error control. We apply our method to publicly available neural data from rats experiencing bouts of non-REM sleep prior to exploration of a radial maze.

Nonlinear Permuted Granger Causality

Granger causal inference is a contentious but widespread method used in fields ranging from economics to neuroscience. The original definition addresses the notion of causality in time series by establishing functional dependence conditional on a specified model. Adaptation of Granger causality to nonlinear data remains challenging, and many methods apply in-sample tests that do not incorporate out-of-sample predictability leading to concerns of model overfitting. To allow for out-of-sample comparison, we explicitly define a measure of functional connectivity using permutations of the covariate set. Artificial neural networks serve as featurizers of the data to approximate any arbitrary, nonlinear relationship, and under certain conditions on the featurization process and the model residuals, we prove consistent estimation of the variance for each permutation. Performance of the permutation method is compared to penalized objective, naive replacement, and omission techniques via simulation, and we investigate its application to neuronal responses of acoustic stimuli in the auditory cortex of anesthetized rats. We contend that targeted use of the Granger causal framework, when prior knowledge of the causal mechanisms in a dataset are limited, can help to reveal potential predictive relationships between sets of variables that warrant further study.

Bridging the Usability Gap: Theoretical and Methodological Advances for Spectral Learning of Hidden Markov Models

The Baum-Welch (B-W) algorithm is the most widely accepted method for inferring hidden Markov models (HMM). However, it is prone to getting stuck in local optima, and can be too slow for many real-time applications. Spectral learning of HMMs (SHMMs), based on the method of moments (MOM) has been proposed in the literature to overcome these obstacles. Despite its promises, asymptotic theory for SHMM has been elusive, and the long-run performance of SHMM can degrade due to unchecked propogation of error. In this paper, we (1) provide an asymptotic distribution for the approximate error of the likelihood estimated by SHMM, and (2) propose a novel algorithm called projected SHMM (PSHMM) that mitigates the problem of error propogation, and (3) develop online learning variantions of both SHMM and PSHMM that accommodate potential nonstationarity. We compare the performance of SHMM with PSHMM and estimation through the B-W algorithm on both simulated data and data from real world applications, and find that PSHMM not only retains the computational advantages of SHMM, but also provides more robust estimation and forecasting.

Trees in transformers: a theoretical analysis of the Transformer's ability to represent trees

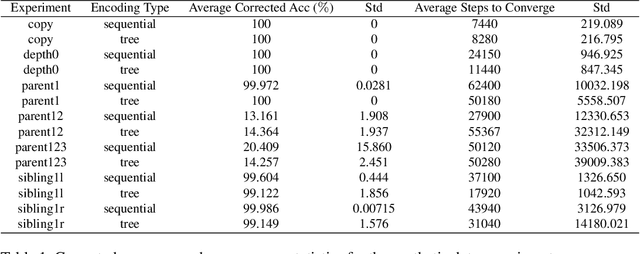
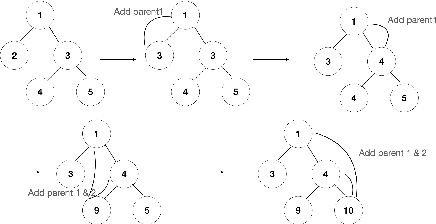
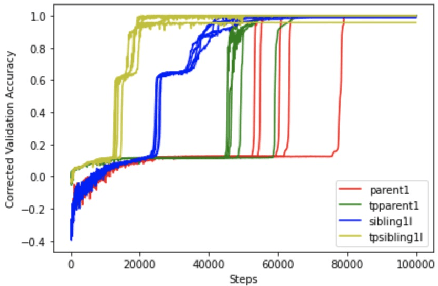
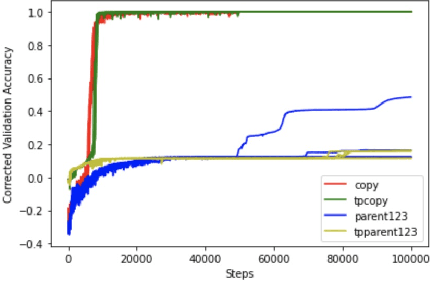
Transformer networks are the de facto standard architecture in natural language processing. To date, there are no theoretical analyses of the Transformer's ability to capture tree structures. We focus on the ability of Transformer networks to learn tree structures that are important for tree transduction problems. We first analyze the theoretical capability of the standard Transformer architecture to learn tree structures given enumeration of all possible tree backbones, which we define as trees without labels. We then prove that two linear layers with ReLU activation function can recover any tree backbone from any two nonzero, linearly independent starting backbones. This implies that a Transformer can learn tree structures well in theory. We conduct experiments with synthetic data and find that the standard Transformer achieves similar accuracy compared to a Transformer where tree position information is explicitly encoded, albeit with slower convergence. This confirms empirically that Transformers can learn tree structures.

Two Step CCA: A new spectral method for estimating vector models of words

Unlabeled data is often used to learn representations which can be used to supplement baseline features in a supervised learner. For example, for text applications where the words lie in a very high dimensional space (the size of the vocabulary), one can learn a low rank "dictionary" by an eigen-decomposition of the word co-occurrence matrix (e.g. using PCA or CCA). In this paper, we present a new spectral method based on CCA to learn an eigenword dictionary. Our improved procedure computes two set of CCAs, the first one between the left and right contexts of the given word and the second one between the projections resulting from this CCA and the word itself. We prove theoretically that this two-step procedure has lower sample complexity than the simple single step procedure and also illustrate the empirical efficacy of our approach and the richness of representations learned by our Two Step CCA (TSCCA) procedure on the tasks of POS tagging and sentiment classification.

Spectral dimensionality reduction for HMMs

Hidden Markov Models (HMMs) can be accurately approximated using co-occurrence frequencies of pairs and triples of observations by using a fast spectral method in contrast to the usual slow methods like EM or Gibbs sampling. We provide a new spectral method which significantly reduces the number of model parameters that need to be estimated, and generates a sample complexity that does not depend on the size of the observation vocabulary. We present an elementary proof giving bounds on the relative accuracy of probability estimates from our model. (Correlaries show our bounds can be weakened to provide either L1 bounds or KL bounds which provide easier direct comparisons to previous work.) Our theorem uses conditions that are checkable from the data, instead of putting conditions on the unobservable Markov transition matrix.