Change Point Detection With Conceptors

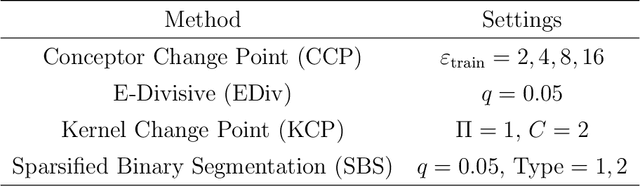
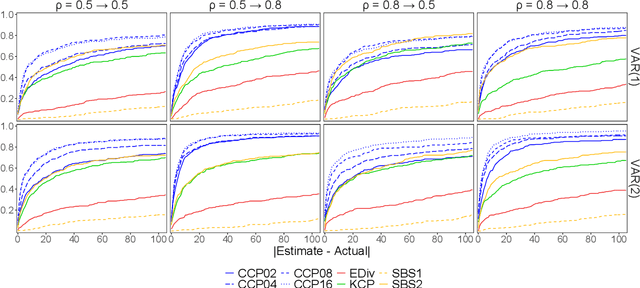
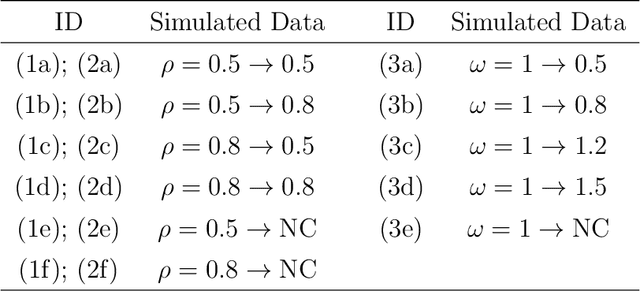
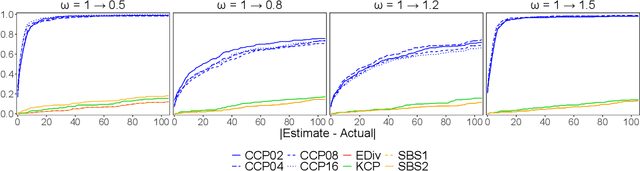
Offline change point detection seeks to identify points in a time series where the data generating process changes. This problem is well studied for univariate i.i.d. data, but becomes challenging with increasing dimension and temporal dependence. For the at most one change point problem, we propose the use of a conceptor matrix to learn the characteristic dynamics of a specified training window in a time series. The associated random recurrent neural network acts as a featurizer of the data, and change points are identified from a univariate quantification of the distance between the featurization and the space spanned by a representative conceptor matrix. This model agnostic method can suggest potential locations of interest that warrant further study. We prove that, under mild assumptions, the method provides a consistent estimate of the true change point, and quantile estimates for statistics are produced via a moving block bootstrap of the original data. The method is tested on simulations from several classes of processes, and we evaluate performance with clustering metrics, graphical methods, and observed Type 1 error control. We apply our method to publicly available neural data from rats experiencing bouts of non-REM sleep prior to exploration of a radial maze.

Nonlinear Permuted Granger Causality

Granger causal inference is a contentious but widespread method used in fields ranging from economics to neuroscience. The original definition addresses the notion of causality in time series by establishing functional dependence conditional on a specified model. Adaptation of Granger causality to nonlinear data remains challenging, and many methods apply in-sample tests that do not incorporate out-of-sample predictability leading to concerns of model overfitting. To allow for out-of-sample comparison, we explicitly define a measure of functional connectivity using permutations of the covariate set. Artificial neural networks serve as featurizers of the data to approximate any arbitrary, nonlinear relationship, and under certain conditions on the featurization process and the model residuals, we prove consistent estimation of the variance for each permutation. Performance of the permutation method is compared to penalized objective, naive replacement, and omission techniques via simulation, and we investigate its application to neuronal responses of acoustic stimuli in the auditory cortex of anesthetized rats. We contend that targeted use of the Granger causal framework, when prior knowledge of the causal mechanisms in a dataset are limited, can help to reveal potential predictive relationships between sets of variables that warrant further study.