Jiwoo Choi
ORIDa: Object-centric Real-world Image Composition Dataset
Jun 10, 2025Abstract:Object compositing, the task of placing and harmonizing objects in images of diverse visual scenes, has become an important task in computer vision with the rise of generative models. However, existing datasets lack the diversity and scale required to comprehensively explore real-world scenarios. We introduce ORIDa (Object-centric Real-world Image Composition Dataset), a large-scale, real-captured dataset containing over 30,000 images featuring 200 unique objects, each of which is presented across varied positions and scenes. ORIDa has two types of data: factual-counterfactual sets and factual-only scenes. The factual-counterfactual sets consist of four factual images showing an object in different positions within a scene and a single counterfactual (or background) image of the scene without the object, resulting in five images per scene. The factual-only scenes include a single image containing an object in a specific context, expanding the variety of environments. To our knowledge, ORIDa is the first publicly available dataset with its scale and complexity for real-world image composition. Extensive analysis and experiments highlight the value of ORIDa as a resource for advancing further research in object compositing.
A 2-step Framework for Automated Literary Translation Evaluation: Its Promises and Pitfalls
Dec 02, 2024Abstract:In this work, we propose and evaluate the feasibility of a two-stage pipeline to evaluate literary machine translation, in a fine-grained manner, from English to Korean. The results show that our framework provides fine-grained, interpretable metrics suited for literary translation and obtains a higher correlation with human judgment than traditional machine translation metrics. Nonetheless, it still fails to match inter-human agreement, especially in metrics like Korean Honorifics. We also observe that LLMs tend to favor translations generated by other LLMs, and we highlight the necessity of developing more sophisticated evaluation methods to ensure accurate and culturally sensitive machine translation of literary works.
MaTableGPT: GPT-based Table Data Extractor from Materials Science Literature
Jun 08, 2024Abstract:Efficiently extracting data from tables in the scientific literature is pivotal for building large-scale databases. However, the tables reported in materials science papers exist in highly diverse forms; thus, rule-based extractions are an ineffective approach. To overcome this challenge, we present MaTableGPT, which is a GPT-based table data extractor from the materials science literature. MaTableGPT features key strategies of table data representation and table splitting for better GPT comprehension and filtering hallucinated information through follow-up questions. When applied to a vast volume of water splitting catalysis literature, MaTableGPT achieved an extraction accuracy (total F1 score) of up to 96.8%. Through comprehensive evaluations of the GPT usage cost, labeling cost, and extraction accuracy for the learning methods of zero-shot, few-shot and fine-tuning, we present a Pareto-front mapping where the few-shot learning method was found to be the most balanced solution owing to both its high extraction accuracy (total F1 score>95%) and low cost (GPT usage cost of 5.97 US dollars and labeling cost of 10 I/O paired examples). The statistical analyses conducted on the database generated by MaTableGPT revealed valuable insights into the distribution of the overpotential and elemental utilization across the reported catalysts in the water splitting literature.
A First-Order Method with Expansive Projection for Optimal Powered Descent Guidance
Sep 30, 2023
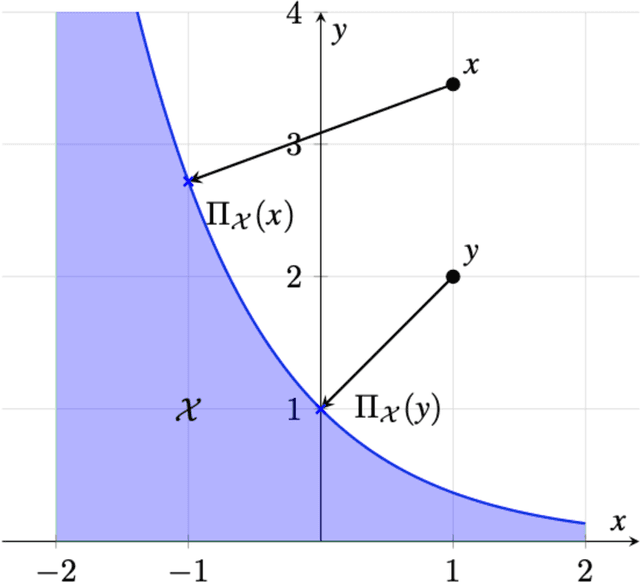
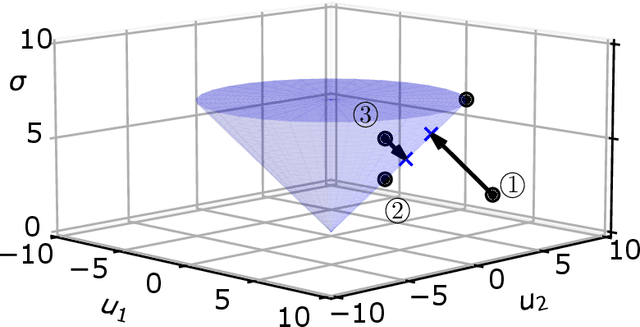
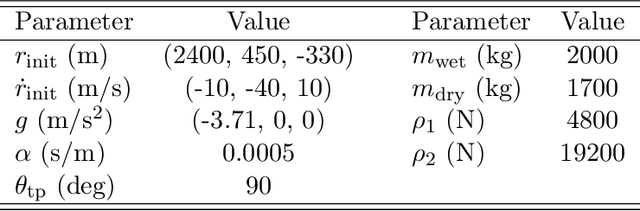
Abstract:This paper introduces a first-order method for solving optimal powered descent guidance (PDG) problems, that directly handles the nonconvex constraints associated with the maximum and minimum thrust bounds with varying mass and the pointing angle constraints on thrust vectors. This issue has been conventionally circumvented via lossless convexification (LCvx), which lifts a nonconvex feasible set to a higher-dimensional convex set, and via linear approximation of another nonconvex feasible set defined by exponential functions. However, this approach sometimes results in an infeasible solution when the solution obtained from the higher-dimensional space is projected back to the original space, especially when the problem involves a nonoptimal time of flight. Additionally, the Taylor series approximation introduces an approximation error that grows with both flight time and deviation from the reference trajectory. In this paper, we introduce a first-order approach that makes use of orthogonal projections onto nonconvex sets, allowing expansive projection (ExProj). We show that 1) this approach produces a feasible solution with better performance even for the nonoptimal time of flight cases for which conventional techniques fail and 2) the proposed method compensates for the linearization error that arises from Taylor series approximation. We claim that the proposed approach offers more flexibility in generating feasible trajectories for a wide variety of planetary soft landing problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge