A First-Order Method with Expansive Projection for Optimal Powered Descent Guidance

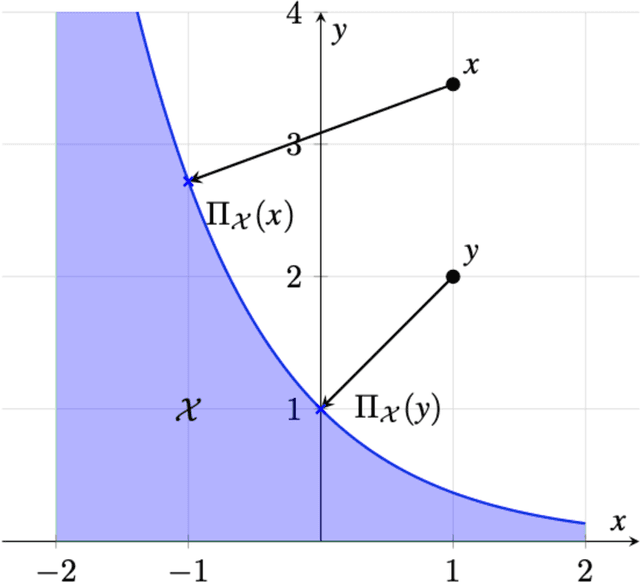
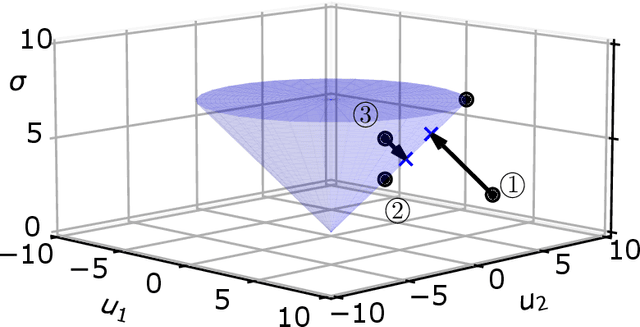
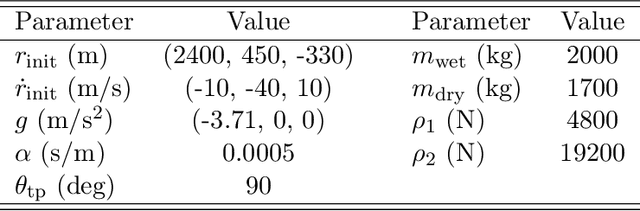
This paper introduces a first-order method for solving optimal powered descent guidance (PDG) problems, that directly handles the nonconvex constraints associated with the maximum and minimum thrust bounds with varying mass and the pointing angle constraints on thrust vectors. This issue has been conventionally circumvented via lossless convexification (LCvx), which lifts a nonconvex feasible set to a higher-dimensional convex set, and via linear approximation of another nonconvex feasible set defined by exponential functions. However, this approach sometimes results in an infeasible solution when the solution obtained from the higher-dimensional space is projected back to the original space, especially when the problem involves a nonoptimal time of flight. Additionally, the Taylor series approximation introduces an approximation error that grows with both flight time and deviation from the reference trajectory. In this paper, we introduce a first-order approach that makes use of orthogonal projections onto nonconvex sets, allowing expansive projection (ExProj). We show that 1) this approach produces a feasible solution with better performance even for the nonoptimal time of flight cases for which conventional techniques fail and 2) the proposed method compensates for the linearization error that arises from Taylor series approximation. We claim that the proposed approach offers more flexibility in generating feasible trajectories for a wide variety of planetary soft landing problems.

Optimal Impact Angle Guidance via First-Order Optimization Under Nonconvex Constraints

Most optimal guidance problems can be formulated as nonconvex optimization problems, which can be solved indirectly by relaxation, convexification, or linearization. Although these methods are guaranteed to converge to the global optimum of the modified problems, the obtained solution may not guarantee global optimality or even the feasibility of the original nonconvex problems. In this paper, we propose a computational optimal guidance approach that directly handles the nonconvex constraints encountered in formulating guidance problems. The proposed computational guidance approach alternately solves the least squares problem and projects the solution onto nonconvex feasible sets, which rapidly converge to feasible suboptimal solutions or, sometimes, to globally optimal solutions. The proposed algorithm is verified via a series of numerical simulations on impact angle guidance problems, and it is demonstrated that the proposed algorithm provides superior guidance performance compared to conventional techniques.