An AI-native experimental laboratory for autonomous biomolecular engineering

Autonomous scientific research, capable of independently conducting complex experiments and serving non-specialists, represents a long-held aspiration. Achieving it requires a fundamental paradigm shift driven by artificial intelligence (AI). While autonomous experimental systems are emerging, they remain confined to areas featuring singular objectives and well-defined, simple experimental workflows, such as chemical synthesis and catalysis. We present an AI-native autonomous laboratory, targeting highly complex scientific experiments for applications like autonomous biomolecular engineering. This system autonomously manages instrumentation, formulates experiment-specific procedures and optimization heuristics, and concurrently serves multiple user requests. Founded on a co-design philosophy of models, experiments, and instruments, the platform supports the co-evolution of AI models and the automation system. This establishes an end-to-end, multi-user autonomous laboratory that handles complex, multi-objective experiments across diverse instrumentation. Our autonomous laboratory supports fundamental nucleic acid functions-including synthesis, transcription, amplification, and sequencing. It also enables applications in fields such as disease diagnostics, drug development, and information storage. Without human intervention, it autonomously optimizes experimental performance to match state-of-the-art results achieved by human scientists. In multi-user scenarios, the platform significantly improves instrument utilization and experimental efficiency. This platform paves the way for advanced biomaterials research to overcome dependencies on experts and resource barriers, establishing a blueprint for science-as-a-service at scale.

Multi: Multimodal Understanding Leaderboard with Text and Images

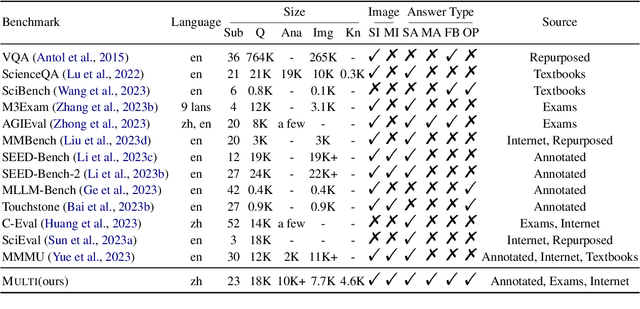
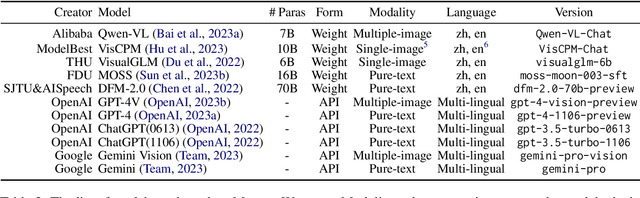
Rapid progress in multimodal large language models (MLLMs) highlights the need to introduce challenging yet realistic benchmarks to the academic community. Existing benchmarks primarily focus on simple natural image understanding, but Multi emerges as a cutting-edge benchmark for MLLMs, offering a comprehensive dataset for evaluating MLLMs against understanding complex figures and tables, and scientific questions. This benchmark, reflecting current realistic examination styles, provides multimodal inputs and requires responses that are either precise or open-ended, similar to real-life school tests. It challenges MLLMs with a variety of tasks, ranging from formula derivation to image detail analysis, and cross-modality reasoning. Multi includes over 18,000 questions, with a focus on science-based QA in diverse formats. We also introduce Multi-Elite, a 500-question subset for testing the extremities of MLLMs, and Multi-Extend, which enhances In-Context Learning research with more than 4,500 knowledge pieces. Our evaluation indicates significant potential for MLLM advancement, with GPT-4V achieving a 63.7% accuracy rate on Multi, in contrast to other MLLMs scoring between 31.3% and 53.7%. Multi serves not only as a robust evaluation platform but also paves the way for the development of expert-level AI.

Supervisory Control of Probabilistic Discrete Event Systems under Partial Observation

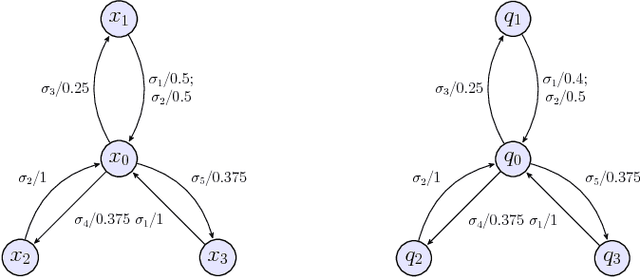
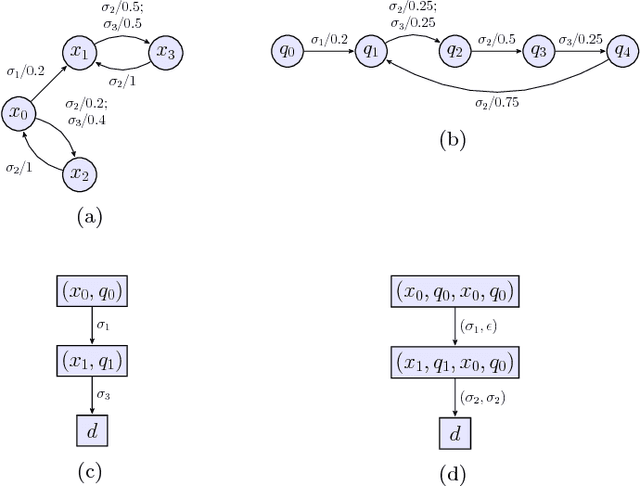
The supervisory control of probabilistic discrete event systems (PDESs) is investigated under the assumptions that the supervisory controller (supervisor) is probabilistic and has a partial observation. The probabilistic P-supervisor is defined, which specifies a probability distribution on the control patterns for each observation. The notions of the probabilistic controllability and observability are proposed and demonstrated to be a necessary and sufficient conditions for the existence of the probabilistic P-supervisors. Moreover, the polynomial verification algorithms for the probabilistic controllability and observability are put forward. In addition, the infimal probabilistic controllable and observable superlanguage is introduced and computed as the solution of the optimal control problem of PDESs. Several examples are presented to illustrate the results obtained.