Supervisory Control of Quantum Discrete Event Systems

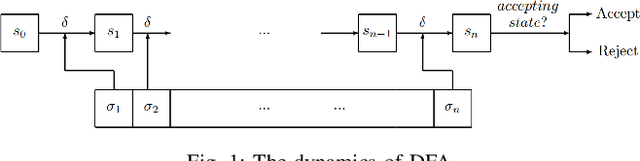
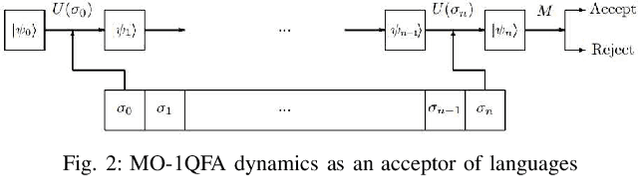
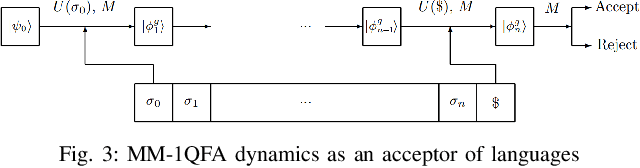
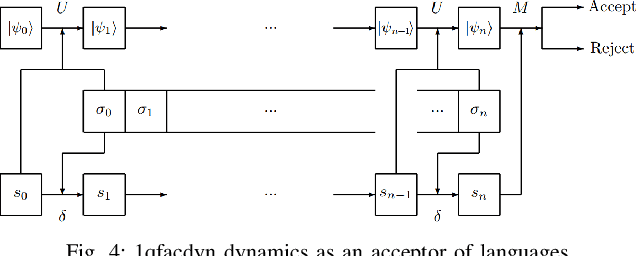
Discrete event systems (DES) have been established and deeply developed in the framework of probabilistic and fuzzy computing models due to the necessity of practical applications in fuzzy and probabilistic systems. With the development of quantum computing and quantum control, a natural problem is to simulate DES by means of quantum computing models and to establish {\it quantum DES} (QDES). The motivation is twofold: on the one hand, QDES have potential applications when DES are simulated and processed by quantum computers, where quantum systems are employed to simulate the evolution of states driven by discrete events, and on the other hand, QDES may have essential advantages over DES concerning state complexity for imitating some practical problems. The goal of this paper is to establish a basic framework of QDES by using {\it quantum finite automata} (QFA) as the modelling formalisms, and the supervisory control theorems of QDES are established and proved. Then we present a polynomial-time algorithm to decide whether or not the controllability condition holds. In particular, we construct a number of new examples of QFA to illustrate the supervisory control of QDES and to verify the essential advantages of QDES over DES in state complexity.

Supervisory Control of Probabilistic Discrete Event Systems under Partial Observation

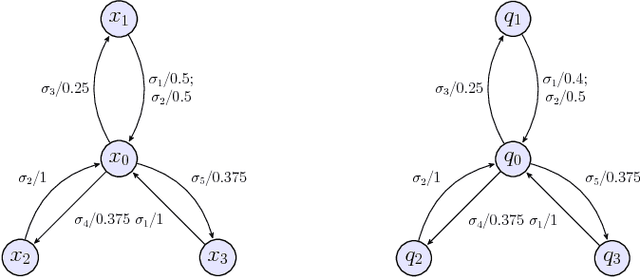
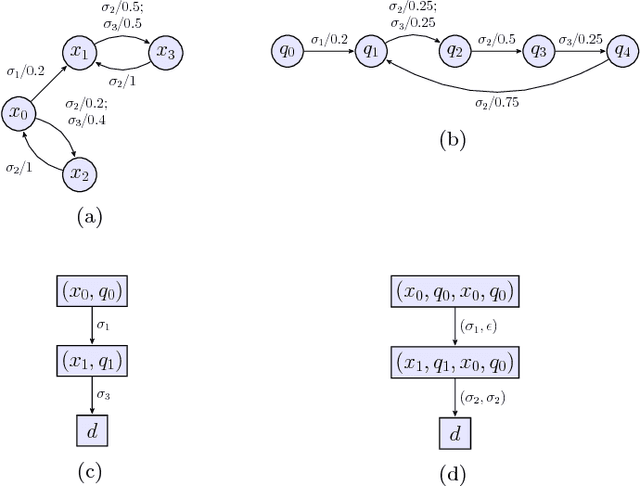
The supervisory control of probabilistic discrete event systems (PDESs) is investigated under the assumptions that the supervisory controller (supervisor) is probabilistic and has a partial observation. The probabilistic P-supervisor is defined, which specifies a probability distribution on the control patterns for each observation. The notions of the probabilistic controllability and observability are proposed and demonstrated to be a necessary and sufficient conditions for the existence of the probabilistic P-supervisors. Moreover, the polynomial verification algorithms for the probabilistic controllability and observability are put forward. In addition, the infimal probabilistic controllable and observable superlanguage is introduced and computed as the solution of the optimal control problem of PDESs. Several examples are presented to illustrate the results obtained.

Diagnosability of Fuzzy Discrete Event Systems

In order to more effectively cope with the real-world problems of vagueness, {\it fuzzy discrete event systems} (FDESs) were proposed recently, and the supervisory control theory of FDESs was developed. In view of the importance of failure diagnosis, in this paper, we present an approach of the failure diagnosis in the framework of FDESs. More specifically: (1) We formalize the definition of diagnosability for FDESs, in which the observable set and failure set of events are {\it fuzzy}, that is, each event has certain degree to be observable and unobservable, and, also, each event may possess different possibility of failure occurring. (2) Through the construction of observability-based diagnosers of FDESs, we investigate its some basic properties. In particular, we present a necessary and sufficient condition for diagnosability of FDESs. (3) Some examples serving to illuminate the applications of the diagnosability of FDESs are described. To conclude, some related issues are raised for further consideration.

Decentralized Failure Diagnosis of Stochastic Discrete Event Systems

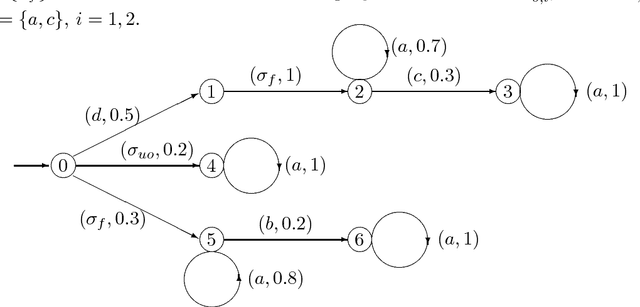
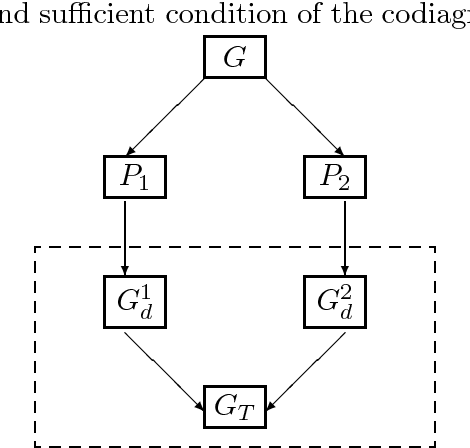
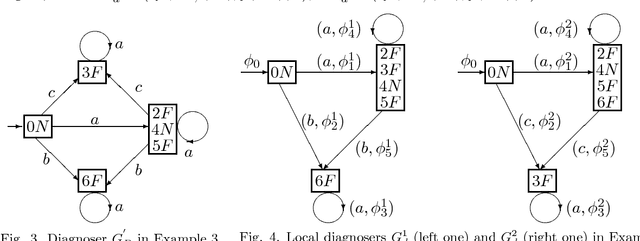
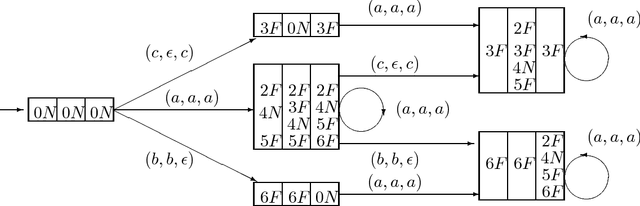
Recently, the diagnosability of {\it stochastic discrete event systems} (SDESs) was investigated in the literature, and, the failure diagnosis considered was {\it centralized}. In this paper, we propose an approach to {\it decentralized} failure diagnosis of SDESs, where the stochastic system uses multiple local diagnosers to detect failures and each local diagnoser possesses its own information. In a way, the centralized failure diagnosis of SDESs can be viewed as a special case of the decentralized failure diagnosis presented in this paper with only one projection. The main contributions are as follows: (1) We formalize the notion of codiagnosability for stochastic automata, which means that a failure can be detected by at least one local stochastic diagnoser within a finite delay. (2) We construct a codiagnoser from a given stochastic automaton with multiple projections, and the codiagnoser associated with the local diagnosers is used to test codiagnosability condition of SDESs. (3) We deal with a number of basic properties of the codiagnoser. In particular, a necessary and sufficient condition for the codiagnosability of SDESs is presented. (4) We give a computing method in detail to check whether codiagnosability is violated. And (5) some examples are described to illustrate the applications of the codiagnosability and its computing method.

Supervisory Control of Fuzzy Discrete Event Systems: A Formal Approach

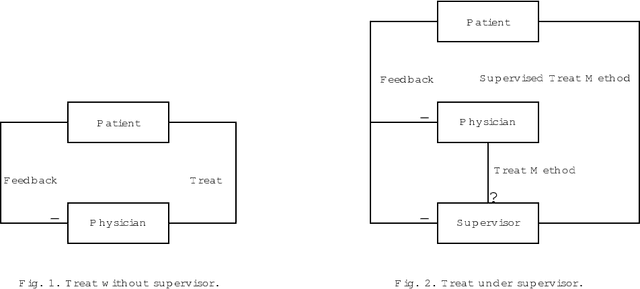
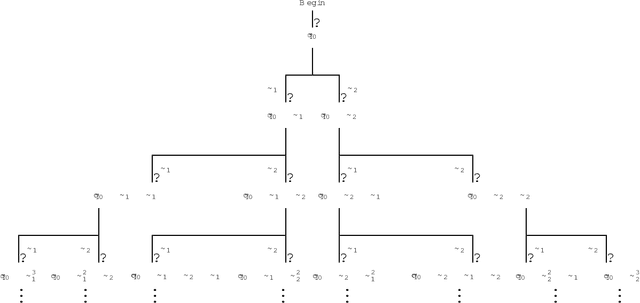
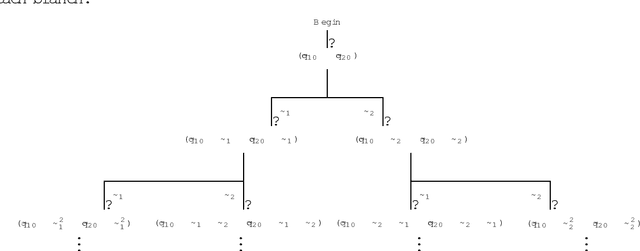
Fuzzy {\it discrete event systems} (DESs) were proposed recently by Lin and Ying [19], which may better cope with the real-world problems with fuzziness, impreciseness, and subjectivity such as those in biomedicine. As a continuation of [19], in this paper we further develop fuzzy DESs by dealing with supervisory control of fuzzy DESs. More specifically, (i) we reformulate the parallel composition of crisp DESs, and then define the parallel composition of fuzzy DESs that is equivalent to that in [19]; {\it max-product} and {\it max-min} automata for modeling fuzzy DESs are considered; (ii) we deal with a number of fundamental problems regarding supervisory control of fuzzy DESs, particularly demonstrate controllability theorem and nonblocking controllability theorem of fuzzy DESs, and thus present the conditions for the existence of supervisors in fuzzy DESs; (iii) we analyze the complexity for presenting a uniform criterion to test the fuzzy controllability condition of fuzzy DESs modeled by max-product automata; in particular, we present in detail a general computing method for checking whether or not the fuzzy controllability condition holds, if max-min automata are used to model fuzzy DESs, and by means of this method we can search for all possible fuzzy states reachable from initial fuzzy state in max-min automata; also, we introduce the fuzzy $n$-controllability condition for some practical problems; (iv) a number of examples serving to illustrate the applications of the derived results and methods are described; some basic properties related to supervisory control of fuzzy DESs are investigated. To conclude, some related issues are raised for further consideration.