From What to How: Attributing CLIP's Latent Components Reveals Unexpected Semantic Reliance

Transformer-based CLIP models are widely used for text-image probing and feature extraction, making it relevant to understand the internal mechanisms behind their predictions. While recent works show that Sparse Autoencoders (SAEs) yield interpretable latent components, they focus on what these encode and miss how they drive predictions. We introduce a scalable framework that reveals what latent components activate for, how they align with expected semantics, and how important they are to predictions. To achieve this, we adapt attribution patching for instance-wise component attributions in CLIP and highlight key faithfulness limitations of the widely used Logit Lens technique. By combining attributions with semantic alignment scores, we can automatically uncover reliance on components that encode semantically unexpected or spurious concepts. Applied across multiple CLIP variants, our method uncovers hundreds of surprising components linked to polysemous words, compound nouns, visual typography and dataset artifacts. While text embeddings remain prone to semantic ambiguity, they are more robust to spurious correlations compared to linear classifiers trained on image embeddings. A case study on skin lesion detection highlights how such classifiers can amplify hidden shortcuts, underscoring the need for holistic, mechanistic interpretability. We provide code at https://github.com/maxdreyer/attributing-clip.

Mechanistic understanding and validation of large AI models with SemanticLens

Unlike human-engineered systems such as aeroplanes, where each component's role and dependencies are well understood, the inner workings of AI models remain largely opaque, hindering verifiability and undermining trust. This paper introduces SemanticLens, a universal explanation method for neural networks that maps hidden knowledge encoded by components (e.g., individual neurons) into the semantically structured, multimodal space of a foundation model such as CLIP. In this space, unique operations become possible, including (i) textual search to identify neurons encoding specific concepts, (ii) systematic analysis and comparison of model representations, (iii) automated labelling of neurons and explanation of their functional roles, and (iv) audits to validate decision-making against requirements. Fully scalable and operating without human input, SemanticLens is shown to be effective for debugging and validation, summarizing model knowledge, aligning reasoning with expectations (e.g., adherence to the ABCDE-rule in melanoma classification), and detecting components tied to spurious correlations and their associated training data. By enabling component-level understanding and validation, the proposed approach helps bridge the "trust gap" between AI models and traditional engineered systems. We provide code for SemanticLens on https://github.com/jim-berend/semanticlens and a demo on https://semanticlens.hhi-research-insights.eu.

Beyond Scalars: Concept-Based Alignment Analysis in Vision Transformers

Vision transformers (ViTs) can be trained using various learning paradigms, from fully supervised to self-supervised. Diverse training protocols often result in significantly different feature spaces, which are usually compared through alignment analysis. However, current alignment measures quantify this relationship in terms of a single scalar value, obscuring the distinctions between common and unique features in pairs of representations that share the same scalar alignment. We address this limitation by combining alignment analysis with concept discovery, which enables a breakdown of alignment into single concepts encoded in feature space. This fine-grained comparison reveals both universal and unique concepts across different representations, as well as the internal structure of concepts within each of them. Our methodological contributions address two key prerequisites for concept-based alignment: 1) For a description of the representation in terms of concepts that faithfully capture the geometry of the feature space, we define concepts as the most general structure they can possibly form - arbitrary manifolds, allowing hidden features to be described by their proximity to these manifolds. 2) To measure distances between concept proximity scores of two representations, we use a generalized Rand index and partition it for alignment between pairs of concepts. We confirm the superiority of our novel concept definition for alignment analysis over existing linear baselines in a sanity check. The concept-based alignment analysis of representations from four different ViTs reveals that increased supervision correlates with a reduction in the semantic structure of learned representations.

Layer-wise Feedback Propagation

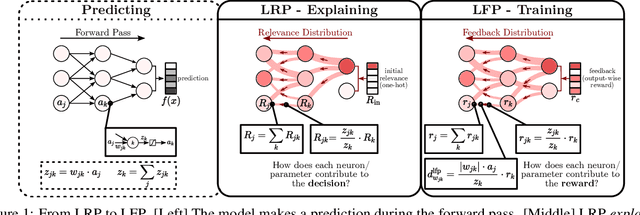
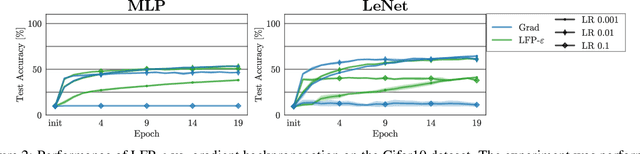
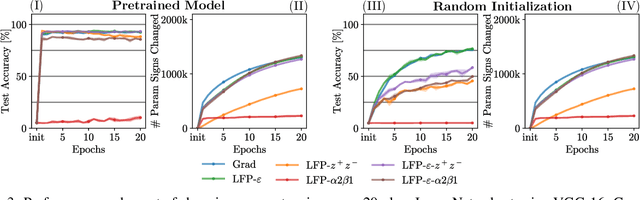
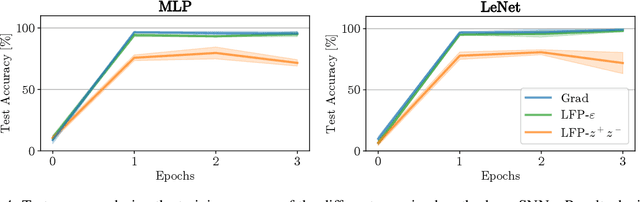
In this paper, we present Layer-wise Feedback Propagation (LFP), a novel training approach for neural-network-like predictors that utilizes explainability, specifically Layer-wise Relevance Propagation(LRP), to assign rewards to individual connections based on their respective contributions to solving a given task. This differs from traditional gradient descent, which updates parameters towards anestimated loss minimum. LFP distributes a reward signal throughout the model without the need for gradient computations. It then strengthens structures that receive positive feedback while reducingthe influence of structures that receive negative feedback. We establish the convergence of LFP theoretically and empirically, and demonstrate its effectiveness in achieving comparable performance to gradient descent on various models and datasets. Notably, LFP overcomes certain limitations associated with gradient-based methods, such as reliance on meaningful derivatives. We further investigate how the different LRP-rules can be extended to LFP, what their effects are on training, as well as potential applications, such as training models with no meaningful derivatives, e.g., step-function activated Spiking Neural Networks (SNNs), or for transfer learning, to efficiently utilize existing knowledge.