Large Language Model is Secretly a Protein Sequence Optimizer

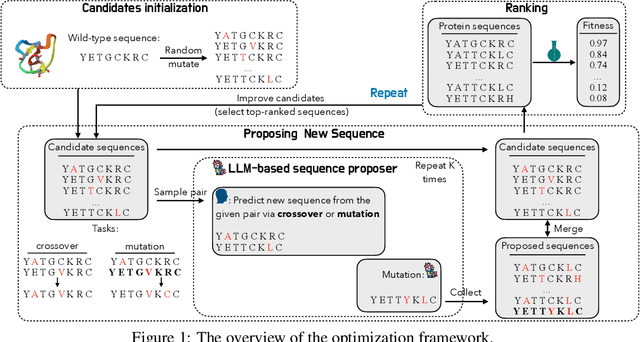
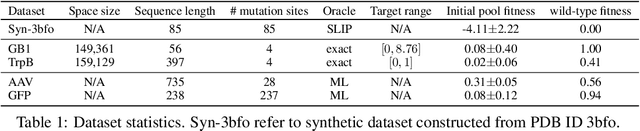
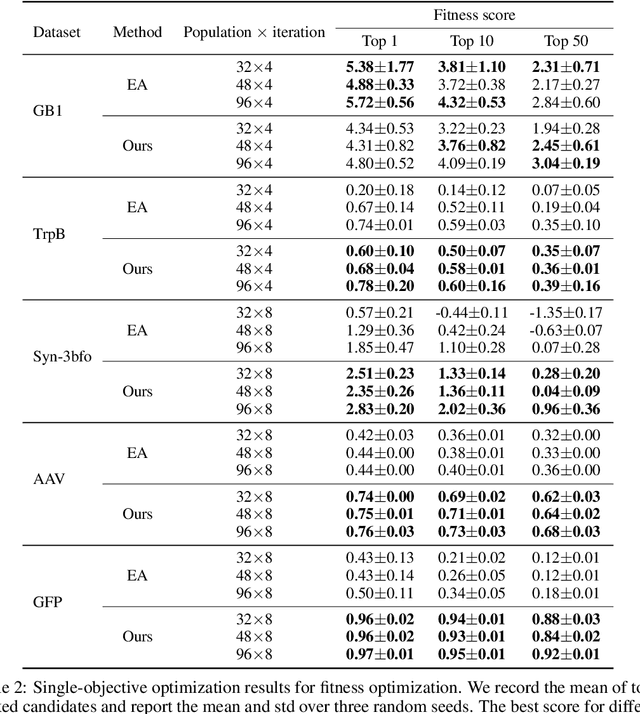
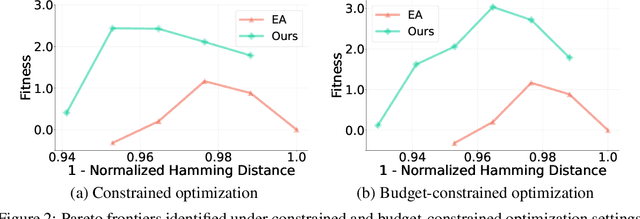
We consider the protein sequence engineering problem, which aims to find protein sequences with high fitness levels, starting from a given wild-type sequence. Directed evolution has been a dominating paradigm in this field which has an iterative process to generate variants and select via experimental feedback. We demonstrate large language models (LLMs), despite being trained on massive texts, are secretly protein sequence optimizers. With a directed evolutionary method, LLM can perform protein engineering through Pareto and experiment-budget constrained optimization, demonstrating success on both synthetic and experimental fitness landscapes.

Graph Generative Pre-trained Transformer

Graph generation is a critical task in numerous domains, including molecular design and social network analysis, due to its ability to model complex relationships and structured data. While most modern graph generative models utilize adjacency matrix representations, this work revisits an alternative approach that represents graphs as sequences of node set and edge set. We advocate for this approach due to its efficient encoding of graphs and propose a novel representation. Based on this representation, we introduce the Graph Generative Pre-trained Transformer (G2PT), an auto-regressive model that learns graph structures via next-token prediction. To further exploit G2PT's capabilities as a general-purpose foundation model, we explore fine-tuning strategies for two downstream applications: goal-oriented generation and graph property prediction. We conduct extensive experiments across multiple datasets. Results indicate that G2PT achieves superior generative performance on both generic graph and molecule datasets. Furthermore, G2PT exhibits strong adaptability and versatility in downstream tasks from molecular design to property prediction.

GraphCroc: Cross-Correlation Autoencoder for Graph Structural Reconstruction

Graph-structured data is integral to many applications, prompting the development of various graph representation methods. Graph autoencoders (GAEs), in particular, reconstruct graph structures from node embeddings. Current GAE models primarily utilize self-correlation to represent graph structures and focus on node-level tasks, often overlooking multi-graph scenarios. Our theoretical analysis indicates that self-correlation generally falls short in accurately representing specific graph features such as islands, symmetrical structures, and directional edges, particularly in smaller or multiple graph contexts. To address these limitations, we introduce a cross-correlation mechanism that significantly enhances the GAE representational capabilities. Additionally, we propose GraphCroc, a new GAE that supports flexible encoder architectures tailored for various downstream tasks and ensures robust structural reconstruction, through a mirrored encoding-decoding process. This model also tackles the challenge of representation bias during optimization by implementing a loss-balancing strategy. Both theoretical analysis and numerical evaluations demonstrate that our methodology significantly outperforms existing self-correlation-based GAEs in graph structure reconstruction.

Mix-GENEO: A flexible filtration for multiparameter persistent homology detects digital images

Two important problems in the field of Topological Data Analysis are defining practical multifiltrations on objects and showing ability of TDA to detect the geometry. Motivated by the problems, we constuct three multifiltrations named multi-GENEO, multi-DGENEO and mix-GENEO, and prove the stability of both the interleaving distance and multiparameter persistence landscape of multi-GENEO with respect to the pseudometric of the subspace of bounded functions. We also give the estimations of upper bound for multi-DGENEO and mix-GENEO. Finally, we provide experiment results on MNIST dataset to demonstrate our bifiltrations have ability to detect geometric and topological differences of digital images.

Efficient and Degree-Guided Graph Generation via Discrete Diffusion Modeling

Diffusion-based generative graph models have been proven effective in generating high-quality small graphs. However, they need to be more scalable for generating large graphs containing thousands of nodes desiring graph statistics. In this work, we propose EDGE, a new diffusion-based generative graph model that addresses generative tasks with large graphs. To improve computation efficiency, we encourage graph sparsity by using a discrete diffusion process that randomly removes edges at each time step and finally obtains an empty graph. EDGE only focuses on a portion of nodes in the graph at each denoising step. It makes much fewer edge predictions than previous diffusion-based models. Moreover, EDGE admits explicitly modeling the node degrees of the graphs, further improving the model performance. The empirical study shows that EDGE is much more efficient than competing methods and can generate large graphs with thousands of nodes. It also outperforms baseline models in generation quality: graphs generated by our approach have more similar graph statistics to those of the training graphs.