Neural Networks for Symbolic Regression

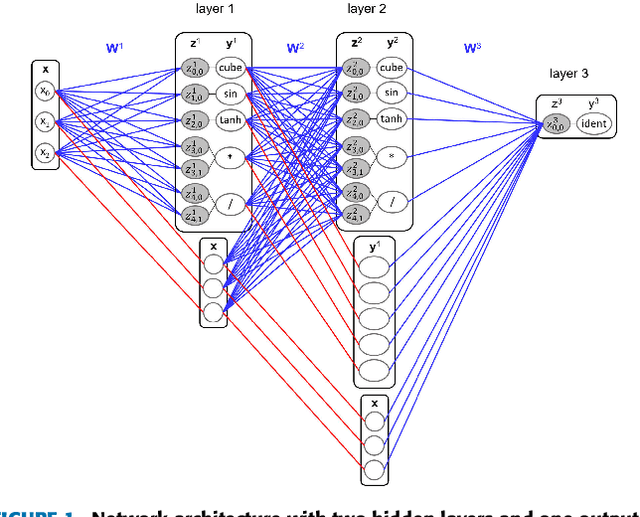
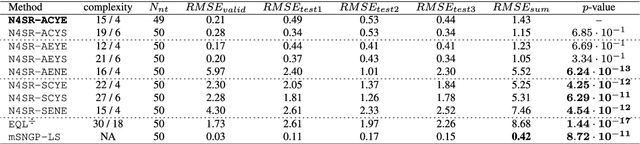
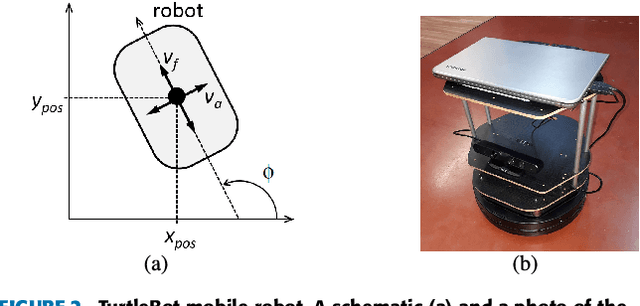
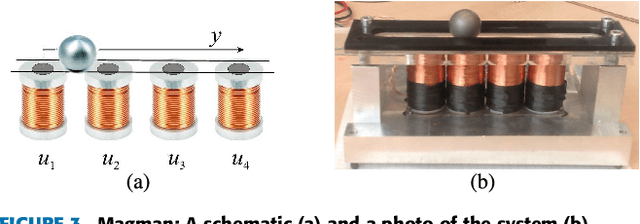
Many real-world systems can be described by mathematical formulas that are human-comprehensible, easy to analyze and can be helpful in explaining the system's behaviour. Symbolic regression is a method that generates nonlinear models from data in the form of analytic expressions. Historically, symbolic regression has been predominantly realized using genetic programming, a method that iteratively evolves a population of candidate solutions that are sampled by genetic operators crossover and mutation. This gradient-free evolutionary approach suffers from several deficiencies: it does not scale well with the number of variables and samples in the training data, models tend to grow in size and complexity without an adequate accuracy gain, and it is hard to fine-tune the inner model coefficients using just genetic operators. Recently, neural networks have been applied to learn the whole analytic formula, i.e., its structure as well as the coefficients, by means of gradient-based optimization algorithms. We propose a novel neural network-based symbolic regression method that constructs physically plausible models based on limited training data and prior knowledge about the system. The method employs an adaptive weighting scheme to effectively deal with multiple loss function terms and an epoch-wise learning process to reduce the chance of getting stuck in poor local optima. Furthermore, we propose a parameter-free method for choosing the model with the best interpolation and extrapolation performance out of all models generated through the whole learning process. We experimentally evaluate the approach on the TurtleBot 2 mobile robot, the magnetic manipulation system, the equivalent resistance of two resistors in parallel, and the anti-lock braking system. The results clearly show the potential of the method to find sparse and accurate models that comply with the prior knowledge provided.

SymFormer: End-to-end symbolic regression using transformer-based architecture

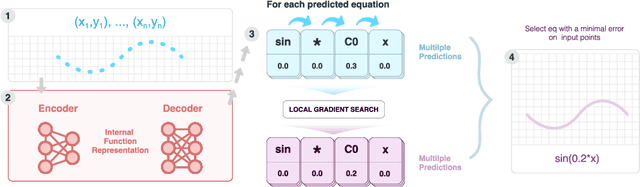
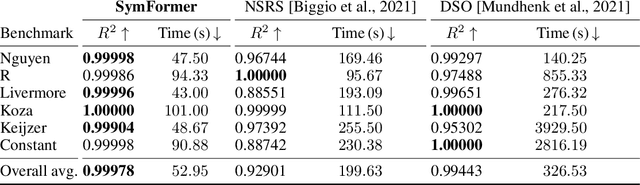
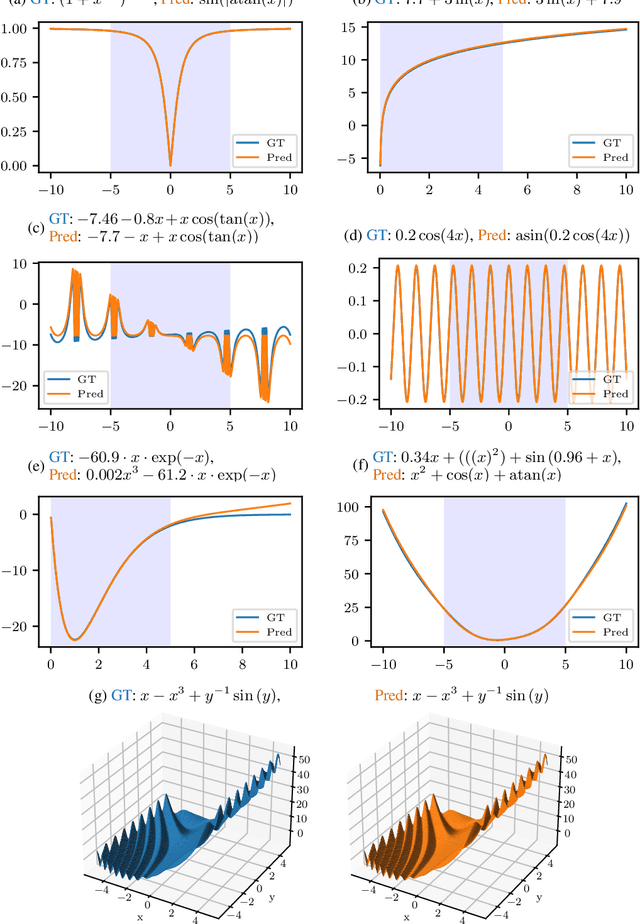
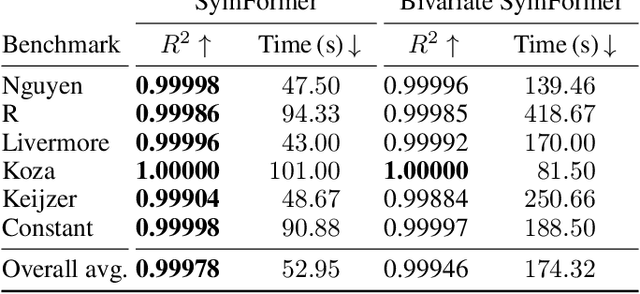
Many real-world problems can be naturally described by mathematical formulas. The task of finding formulas from a set of observed inputs and outputs is called symbolic regression. Recently, neural networks have been applied to symbolic regression, among which the transformer-based ones seem to be the most promising. After training the transformer on a large number of formulas (in the order of days), the actual inference, i.e., finding a formula for new, unseen data, is very fast (in the order of seconds). This is considerably faster than state-of-the-art evolutionary methods. The main drawback of transformers is that they generate formulas without numerical constants, which have to be optimized separately, so yielding suboptimal results. We propose a transformer-based approach called SymFormer, which predicts the formula by outputting the individual symbols and the corresponding constants simultaneously. This leads to better performance in terms of fitting the available data. In addition, the constants provided by SymFormer serve as a good starting point for subsequent tuning via gradient descent to further improve the performance. We show on a set of benchmarks that SymFormer outperforms two state-of-the-art methods while having faster inference.

An Integrated Approach to Goal Selection in Mobile Robot Exploration

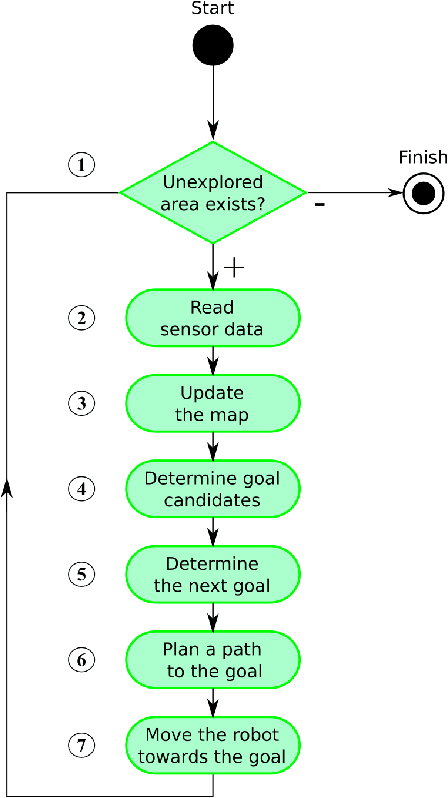
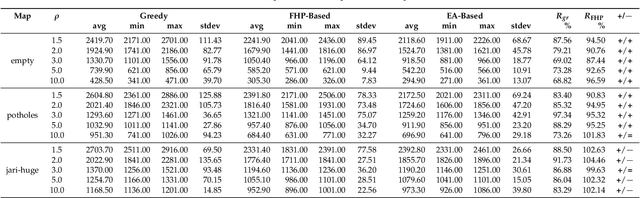
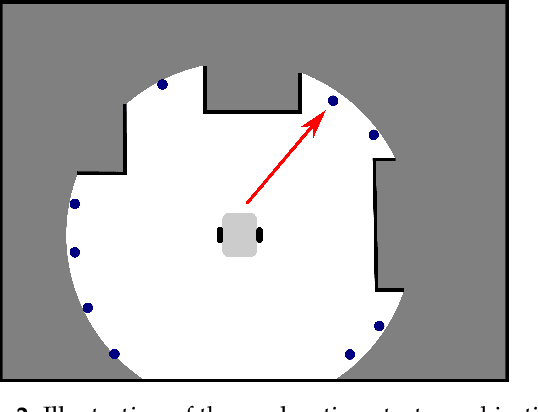
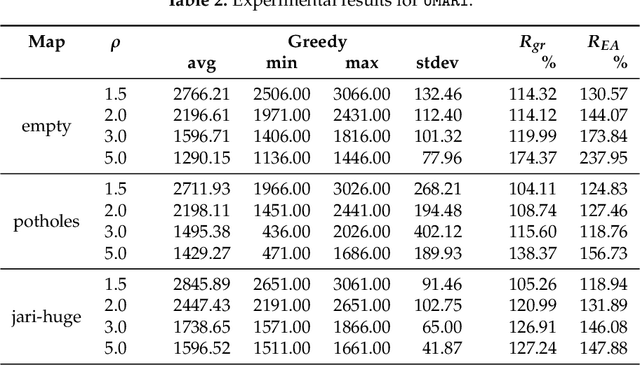
This paper deals with the problem of autonomous navigation of a mobile robot in an unknown 2D environment to fully explore the environment as efficiently as possible. We assume a terrestrial mobile robot equipped with a ranging sensor with a limited range and 360 degrees field of view. The key part of the exploration process is formulated as the d-Watchman Route Problem which consists of two coupled tasks - candidate goals generation and finding an optimal path through a subset of goals - which are solved in each exploration step. The latter has been defined as a constrained variant of the Generalized Traveling Salesman Problem and solved using an evolutionary algorithm. An evolutionary algorithm that uses an indirect representation and the nearest neighbor based constructive procedure was proposed to solve this problem. Individuals evolved in this evolutionary algorithm do not directly code the solutions to the problem. Instead, they represent sequences of instructions to construct a feasible solution. The problems with efficiently generating feasible solutions typically arising when applying traditional evolutionary algorithms to constrained optimization problems are eliminated this way. The proposed exploration framework was evaluated in a simulated environment on three maps and the time needed to explore the whole environment was compared to state-of-the-art exploration methods. Experimental results show that our method outperforms the compared ones in environments with a low density of obstacles by up to 12.5%, while it is slightly worse in office-like environments by 4.5% at maximum. The framework has also been deployed on a real robot to demonstrate the applicability of the proposed solution with real hardware.

Symbolic Regression for Constructing Analytic Models in Reinforcement Learning

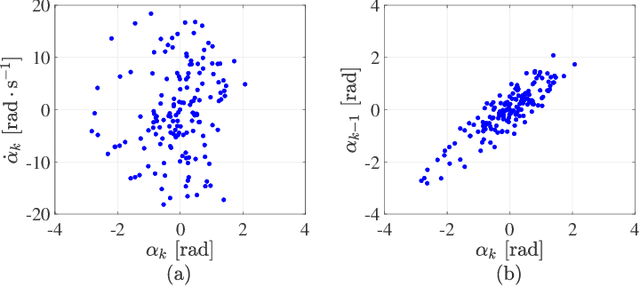
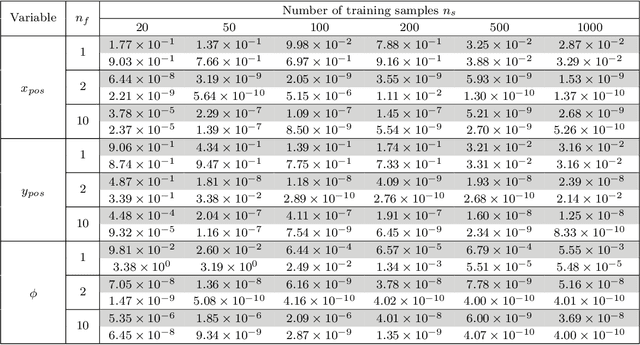
Reinforcement learning (RL) is a widely used approach for controlling systems with unknown or time-varying dynamics. Even though RL does not require a model of the system, it is known to be faster and safer when using models learned online. We propose to employ symbolic regression (SR) to construct parsimonious process models described by analytic equations for real-time RL control. We have tested our method with two different state-of-the-art SR algorithms which automatically search for equations that fit the measured data. In addition to the standard problem formulation in the state-space domain, we show how the method can also be applied to input-output models of the NARX (nonlinear autoregressive with exogenous input) type. We present the approach on three simulated examples with up to 14-dimensional state space: an inverted pendulum, a mobile robot, and a biped walking robot. A comparison with deep neural networks and local linear regression shows that SR in most cases outperforms these commonly used alternative methods. We demonstrate on a real pendulum system that the analytic model found enables RL to successfully perform the swing-up task, based on a model constructed from only 100 data samples.

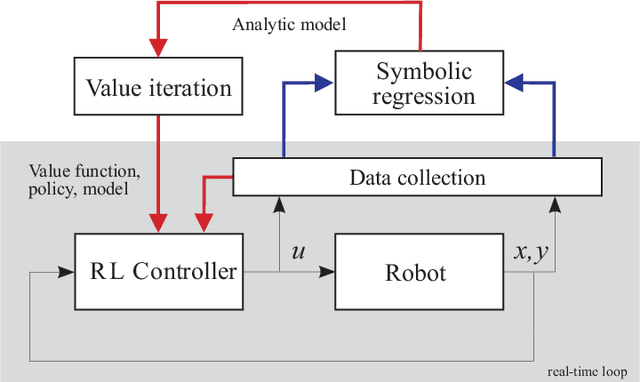
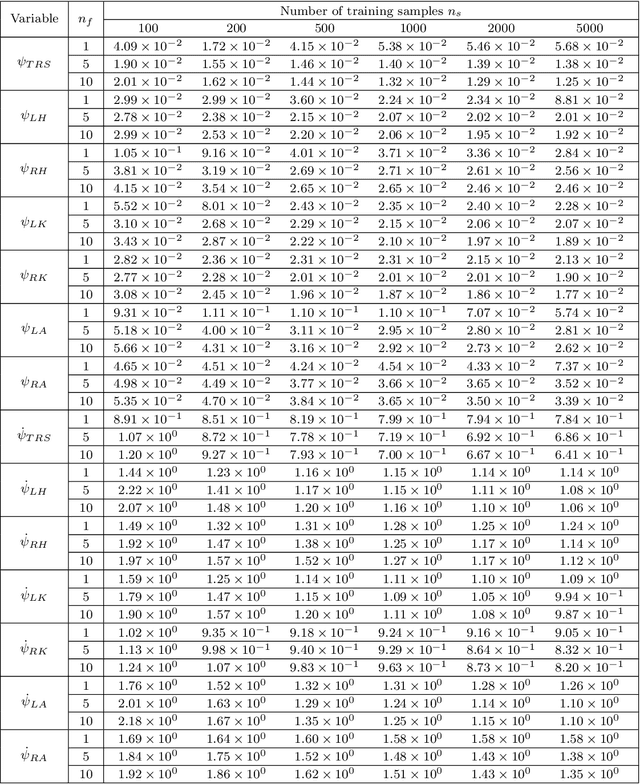
Symbolic Regression Methods for Reinforcement Learning

Reinforcement learning algorithms can be used to optimally solve dynamic decision-making and control problems. With continuous-valued state and input variables, reinforcement learning algorithms must rely on function approximators to represent the value function and policy mappings. Commonly used numerical approximators, such as neural networks or basis function expansions, have two main drawbacks: they are black-box models offering no insight in the mappings learned, and they require significant trial and error tuning of their meta-parameters. In this paper, we propose a new approach to constructing smooth value functions by means of symbolic regression. We introduce three off-line methods for finding value functions based on a state transition model: symbolic value iteration, symbolic policy iteration, and a direct solution of the Bellman equation. The methods are illustrated on four nonlinear control problems: velocity control under friction, one-link and two-link pendulum swing-up, and magnetic manipulation. The results show that the value functions not only yield well-performing policies, but also are compact, human-readable and mathematically tractable. This makes them potentially suitable for further analysis of the closed-loop system. A comparison with alternative approaches using neural networks shows that our method constructs well-performing value functions with substantially fewer parameters.