Symbolic Regression Methods for Reinforcement Learning

Reinforcement learning algorithms can be used to optimally solve dynamic decision-making and control problems. With continuous-valued state and input variables, reinforcement learning algorithms must rely on function approximators to represent the value function and policy mappings. Commonly used numerical approximators, such as neural networks or basis function expansions, have two main drawbacks: they are black-box models offering no insight in the mappings learned, and they require significant trial and error tuning of their meta-parameters. In this paper, we propose a new approach to constructing smooth value functions by means of symbolic regression. We introduce three off-line methods for finding value functions based on a state transition model: symbolic value iteration, symbolic policy iteration, and a direct solution of the Bellman equation. The methods are illustrated on four nonlinear control problems: velocity control under friction, one-link and two-link pendulum swing-up, and magnetic manipulation. The results show that the value functions not only yield well-performing policies, but also are compact, human-readable and mathematically tractable. This makes them potentially suitable for further analysis of the closed-loop system. A comparison with alternative approaches using neural networks shows that our method constructs well-performing value functions with substantially fewer parameters.

Learning Linear Feature Space Transformations in Symbolic Regression

We propose a new type of leaf node for use in Symbolic Regression (SR) that performs linear combinations of feature variables (LCF). These nodes can be handled in three different modes -- an unsynchronized mode, where all LCFs are free to change on their own, a synchronized mode, where LCFs are sorted into groups in which they are forced to be identical throughout the whole individual, and a globally synchronized mode, which is similar to the previous mode but the grouping is done across the whole population. We also present two methods of evolving the weights of the LCFs -- a purely stochastic way via mutation and a gradient-based way based on the backpropagation algorithm known from neural networks -- and also a combination of both. We experimentally evaluate all configurations of LCFs in Multi-Gene Genetic Programming (MGGP), which was chosen as baseline, on a number of benchmarks. According to the results, we identified two configurations which increase the performance of the algorithm.

Symbolic Regression Algorithms with Built-in Linear Regression

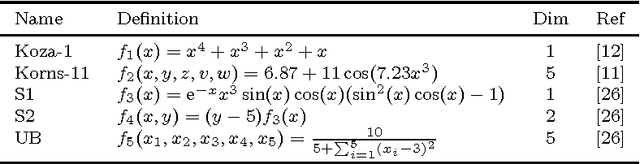
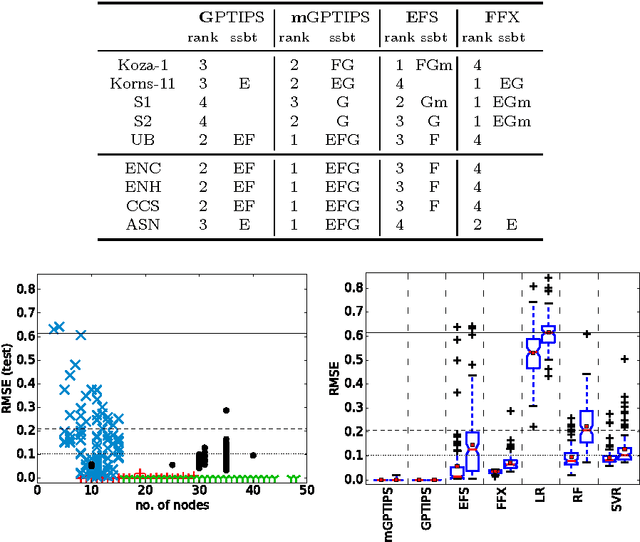
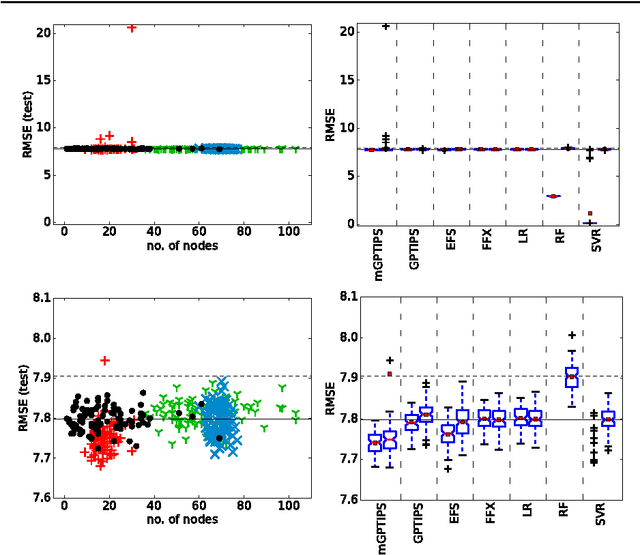
Recently, several algorithms for symbolic regression (SR) emerged which employ a form of multiple linear regression (LR) to produce generalized linear models. The use of LR allows the algorithms to create models with relatively small error right from the beginning of the search; such algorithms are thus claimed to be (sometimes by orders of magnitude) faster than SR algorithms based on vanilla genetic programming. However, a systematic comparison of these algorithms on a common set of problems is still missing. In this paper we conceptually and experimentally compare several representatives of such algorithms (GPTIPS, FFX, and EFS). They are applied as off-the-shelf, ready-to-use techniques, mostly using their default settings. The methods are compared on several synthetic and real-world SR benchmark problems. Their performance is also related to the performance of three conventional machine learning algorithms --- multiple regression, random forests and support vector regression.

Model Selection and Overfitting in Genetic Programming: Empirical Study [Extended Version]

Genetic Programming has been very successful in solving a large area of problems but its use as a machine learning algorithm has been limited so far. One of the reasons is the problem of overfitting which cannot be solved or suppresed as easily as in more traditional approaches. Another problem, closely related to overfitting, is the selection of the final model from the population. In this article we present our research that addresses both problems: overfitting and model selection. We compare several ways of dealing with ovefitting, based on Random Sampling Technique (RST) and on using a validation set, all with an emphasis on model selection. We subject each approach to a thorough testing on artificial and real--world datasets and compare them with the standard approach, which uses the full training data, as a baseline.