Symbolic Regression Algorithms with Built-in Linear Regression
Paper and Code
Mar 10, 2017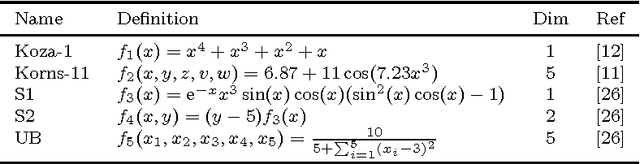
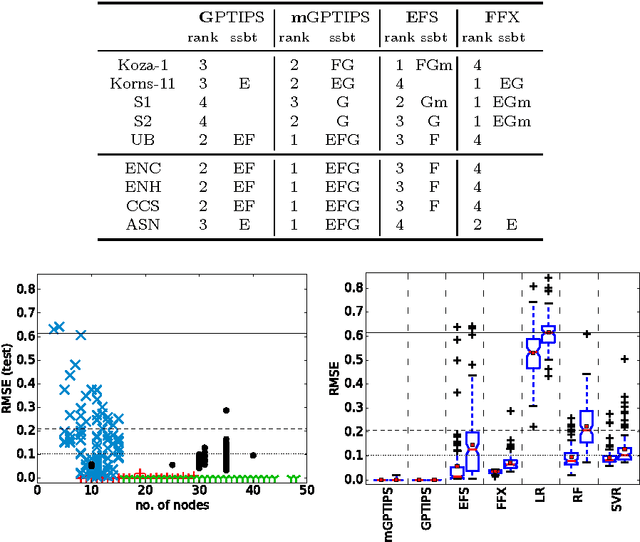

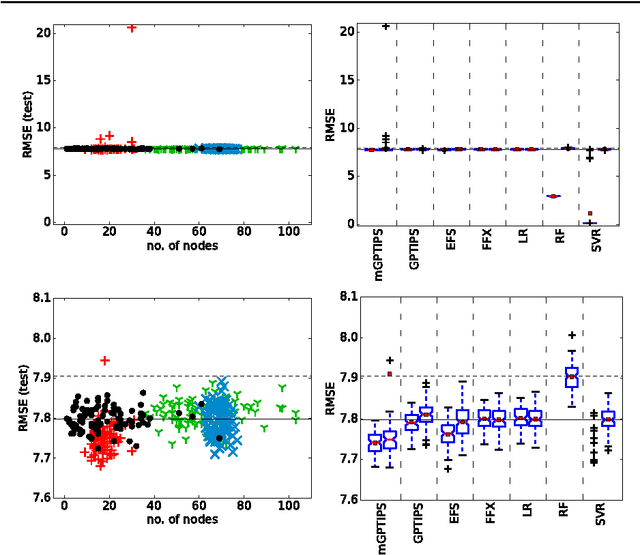
Recently, several algorithms for symbolic regression (SR) emerged which employ a form of multiple linear regression (LR) to produce generalized linear models. The use of LR allows the algorithms to create models with relatively small error right from the beginning of the search; such algorithms are thus claimed to be (sometimes by orders of magnitude) faster than SR algorithms based on vanilla genetic programming. However, a systematic comparison of these algorithms on a common set of problems is still missing. In this paper we conceptually and experimentally compare several representatives of such algorithms (GPTIPS, FFX, and EFS). They are applied as off-the-shelf, ready-to-use techniques, mostly using their default settings. The methods are compared on several synthetic and real-world SR benchmark problems. Their performance is also related to the performance of three conventional machine learning algorithms --- multiple regression, random forests and support vector regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge