Symbolic Regression for Constructing Analytic Models in Reinforcement Learning
Paper and Code
Mar 27, 2019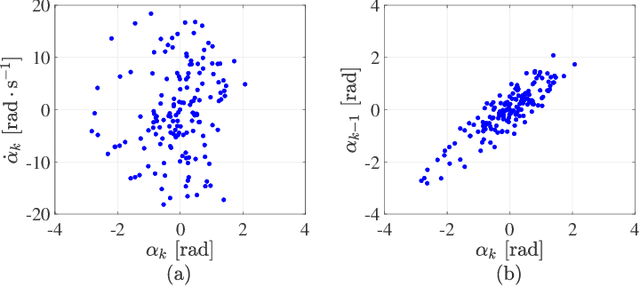
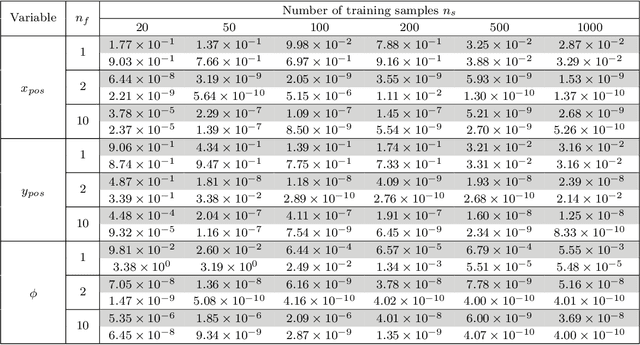
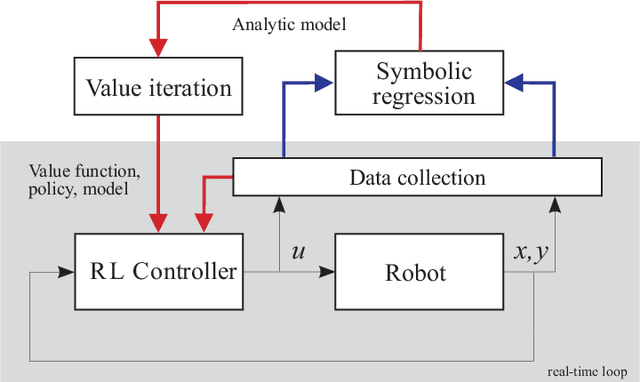
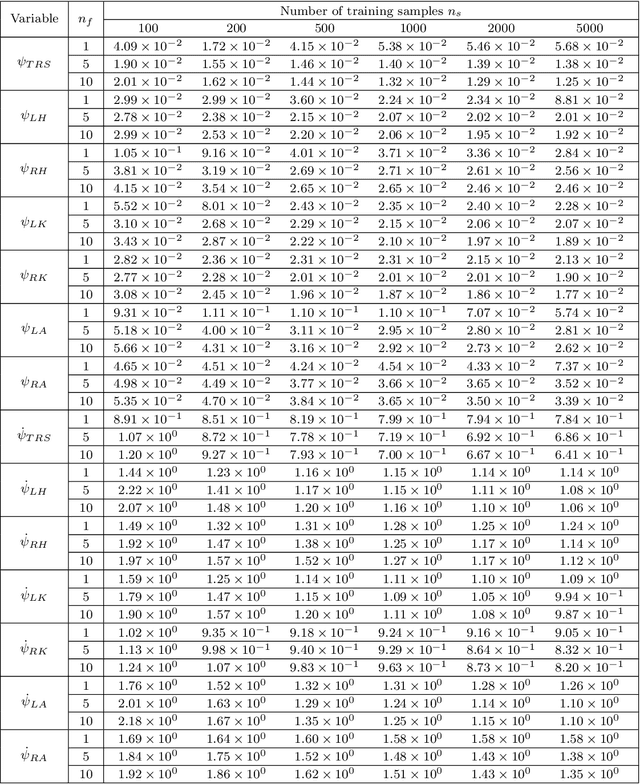
Reinforcement learning (RL) is a widely used approach for controlling systems with unknown or time-varying dynamics. Even though RL does not require a model of the system, it is known to be faster and safer when using models learned online. We propose to employ symbolic regression (SR) to construct parsimonious process models described by analytic equations for real-time RL control. We have tested our method with two different state-of-the-art SR algorithms which automatically search for equations that fit the measured data. In addition to the standard problem formulation in the state-space domain, we show how the method can also be applied to input-output models of the NARX (nonlinear autoregressive with exogenous input) type. We present the approach on three simulated examples with up to 14-dimensional state space: an inverted pendulum, a mobile robot, and a biped walking robot. A comparison with deep neural networks and local linear regression shows that SR in most cases outperforms these commonly used alternative methods. We demonstrate on a real pendulum system that the analytic model found enables RL to successfully perform the swing-up task, based on a model constructed from only 100 data samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge